Um pequeno bloco de massa está submetido a uma única força resultante que é aplicada paralelamente ao eixo escolhido como . Sabe-se que quando se encontra na posição o bloco está em repouso. A componente de é dada pelo gráfico.
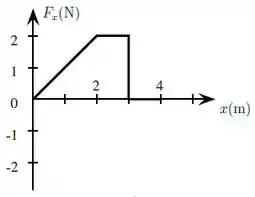
Qual o trabalho exercido pela força no deslocamento da posição até ?
(a)
(b)
(c)
(d)
(e)
Passo 1
O trabalho de uma força é:
Sabemos que a força está na mesma direção e sentido do deslocamento, então:
Mas calma lá... a gente usava essa expressão quando tínhamos uma força constante.
Nesse caso, a força está variando conforme o deslocamento .
Então, vamos utilizar a nossa querida integral:
Aí a gente já começa a lembrar do cálculo e já bate um desespero...

Mas fica tranquilo que a gente tem uma saída muito tranquila pra essa integral.
Passo 2
Queremos o trabalho da força entre os instantes e , então esses vão ser os intervalos da nossa integral:
Passo 3
Uma integral resulta na área abaixo do gráfico, ou seja, nós podemos simplesmente calcular a área abaixo do gráfico para achar o trabalho :
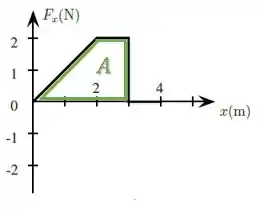
OBS: De até , a força é nula e não gera trabalho.
Podemos dividir essa área em um triângulo e um retângulo, ou então calcular diretamente a área do trapézio.
Vamos dividir em um triângulo e um retângulo:
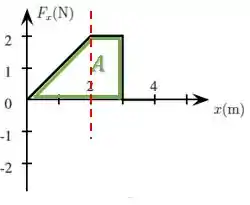
Ficamos com a alternativa (d).
Resposta
Letra (d)