Exercícios Resolvidos de Trabalho de uma Força Variável

Exercício 29 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 30 31 32 33 34 35 36 37 38 39

Enunciado

Halliday - Vol.1 - Ed. 8 - Capítulo 7 – Seção 8 – Questão 34

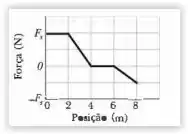
(Capítulo 7.8 – Exercício 34) Um bloco de se move em uma linha reta sobre uma superfície horizontal sem atrito sob a influência de uma força que varia com a posição, como mostra a Fig. 7-38. A escala vertical do gráfico é definida por . Qual é o trabalho realizado pela força quando o bloco se desloca da origem até ?

Passo 1

Faala galera, vamos lá pra mais uma!

Sabemos que a área sob a curva igual ao trabalho realizado, certo? Então vamos usar o gráfico dado ao nosso favor, calculando a área sob o gráfico que foi dado 😉

Passo 2

Calculando a área a partir das expressões da área de um retângulo () e da área de um triângulo , obtemos que :

Temos que

- Para , temos um retângulo de base 2 e altura

- Para , temos um triângulo de base 2 e altura

- Para , não há força exercida (repara que tá na linha )

- Para , temos um triângulo negativo de base 2 e altura

Calculando as áreas que correspondem aos valores dos trabalhos em cada intervalo, temos que:

Substituindo :

E é isso aíí

Resposta

Exercícios de Livros Relacionados

Um bloco de 5,0k g se move em uma linha reta sobre uma superfície horizontal sem atrito sob a influência de uma força que varia com a posição, como mostra a Fig. 7-38. A escala vertical do gráfico é d

Uma força F=c x -3,00 x 2 i → , onde F está em newtons, x em metros e e é uma constante, age sobre uma partícula que se desloca ao longo de um eixo x . Em x= 0 , a energia cinética da partícula é 20,0

Uma única força atua sobre um objeto de 3,0k g que se comporta como uma partícula, de tal forma que a posição do objeto em função do tempo é dada por x=3,0 t - 4,0 t 2+1,0 t 3 , com x em metros e t em

60. Uma partícula de massa m parte de x 0 = 0m com v 00m / s . Ao se mover para a direita sobre o eixo x , a partícula experimenta uma força variável dada por F x = F 0 sen ⁡ ( c x ) , onde F 0 e c sã

Uma força de 160N estica 0,050m uma certa mola a partir do seu comprimento sem deformação. a) Qual é a força necessária para esticar essa mola 0,015m a partir do seu comprimento sem deformação? E para