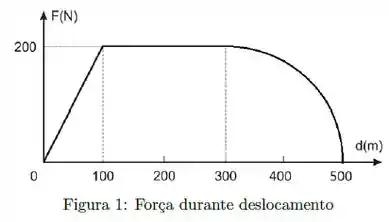
Calcule o trabalho realizado pela força mostrada na figura 1, durante o deslocamento de a metros. Considere o trecho da curva entre e metros como perfeitamente circular. (“” significa "vezes mil".)
(A) ;
(B) ;
(C) ;
(D) ;
(E) ;
Passo 1
Queremos calcular o trabalho de uma força ao longo do deslocamento de a metros.
Beleza!
Talvez a primeira maneira de fazer isso que venha na cabeça é:
Já sabemos o deslocamento , mas qual é o valor da força ?
Essa fórmula ai de cima pode ser usada quando achamos um valor médio de , então a gente acaba usando ela quando é constante.
Mas em brincadeira de gente grande, a força não costuma ser constante, né.
Então temos que usar a queridinha integral:
Com essa integral conseguimos calcular o trabalho de uma força variável se tivermos o gráfico dessa força, como é o caso da questão.
Então, basta nós calcularmos o trabalho de por meio da integral da força ao longo do deslocamento de a metros:
Ahh, entendi...

Mas relaxa, não vai complicar que nem em cálculo não hahaha.
Lembra que a integral de uma função nos dá a área abaixo da curva?
Então, na verdade, basta a gente calcular a área abaixo da curva desse gráfico que achamos o trabalho.
Ah, ufaaa.
Passo 2
Vamos dividir o gráfico em 3 regiões:
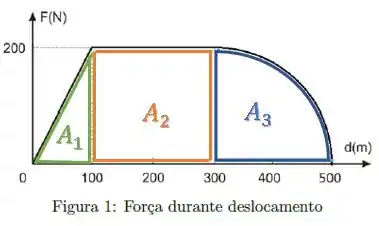
A integral da força pode ser calculada pela área:
é a área do triângulo de base e altura :
A área é a área de um retângulo de lados iguais (famoso quadrado, só vi agora hahah):
Enquanto será a área de um quarto de círculo:
O raio do círculo é :
Passo 3
Somando essas coisas todas, temos:
Show, então, já achamos o trabalho:
Esse podemos escrever como :
Além disso, podemos botar em evidência:
Pronto, achamos a resposta da letra (E).
Resposta
Letra (E)