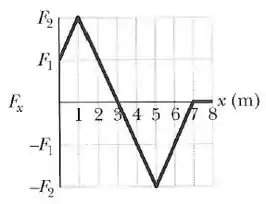
Uma partícula move-se ao longo do eixo sob a ação da força representada no gráfico abaixo. A partícula parte do repouso em . Para posições entre e , a energia cinética da partícula é máxima quando
(A)
(B)
(C)
(D)
(E)
Passo 1
Primeiro de tudo, lembra que o trabalho de uma força variável é dado pela integral da força ao longo do deslocamento?

Putz, essa história de integral ai já tá me confundindo. Calma, calma.
Essa integral é nada mais do que a área abaixo da curva naquele gráfico.
Ahhhhh, saquei.
Mas pera, e o que eu faço com esse trabalho?
Queremos a energia cinética, então podemos usar o teorema trabalho-energia cinética:
Passo 2
Então vamos analisar esse trabalho em cada trecho.
O corpo parte do repouso e recebe uma força positiva entre até , então sua velocidade vai aumentar até .
O trabalho da força será essa área aqui:

Como a partícula parte do repouso, sua energia cinética será:
Vimos que a energia cinética foi aumentando até , quando a força passa a ser negativa e começa a agir contra o movimento.
Como a força agora é negativa , seu trabalho também será negativo.
Então, vamos lá. Se o corpo foi ganhando velocidade (energia cinética) por meio da força positiva até e após essa posição ele passa a receber uma força negativa, diminuindo sua velocidade e consequentemente sua energia cinética, então, o valor máximo de será antes dessa diminuição, ou seja, em .
Resposta
Letra (B)