Exercícios Resolvidos de Trabalho de uma Força Variável

Exercício 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39

Enunciado

UNICAMP 2019.1, P2 – Questão 1: Energia Potencial Gravitacional

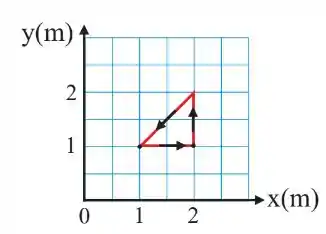
Um carrinho está sobre ação da Força:, enquanto se move em um trilho com a forma indicada na figura. Ao percorrer o caminho fechado (1, 1) → (2, 1) → (2, 2) → (1, 1), o trabalho realizado pela força é:

a) W = 0 J.

b) W = +21 J.

c) W = -24 J.

d) W = +27 J.

e) W = -37 J.

Passo 1

Bom, o nosso trabalho total vai ser a soma de todos os trabalhos, ok? Então:

Como sabemos, o trabalho é a integral da força, então vamos fazer isso pra cada caminho, analisando se o caminho ta na horizontal (x), vertical (y) ou na diagonal (x+y). Sendo e , o primeiro caso só temos o movimento horizontal com y=1, então:

No segundo, temos só horizontal, com x=2, então:

E no terceiro... Como temos um trecho em diagonal, temos que neste trecho x = y, e portanto e , e assim:

Então o trabalho total seria... TARAM: W = −3 + 32 − 8 = 21J

Showwww!

Resposta

b) 21J

Exercícios de Livros Relacionados

Um bloco de 5,0k g se move em uma linha reta sobre uma superfície horizontal sem atrito sob a influência de uma força que varia com a posição, como mostra a Fig. 7-38. A escala vertical do gráfico é d

Uma força F=c x -3,00 x 2 i → , onde F está em newtons, x em metros e e é uma constante, age sobre uma partícula que se desloca ao longo de um eixo x . Em x= 0 , a energia cinética da partícula é 20,0

Uma única força atua sobre um objeto de 3,0k g que se comporta como uma partícula, de tal forma que a posição do objeto em função do tempo é dada por x=3,0 t - 4,0 t 2+1,0 t 3 , com x em metros e t em

60. Uma partícula de massa m parte de x 0 = 0m com v 00m / s . Ao se mover para a direita sobre o eixo x , a partícula experimenta uma força variável dada por F x = F 0 sen ⁡ ( c x ) , onde F 0 e c sã

Uma força de 160N estica 0,050m uma certa mola a partir do seu comprimento sem deformação. a) Qual é a força necessária para esticar essa mola 0,015m a partir do seu comprimento sem deformação? E para