Uma mola, ao ser comprimida, tem uma resposta não-linear, dada por uma força (errata), onde os coeficientes são e . Partindo da posição de máxima compressão , a mola realiza trabalho sobre um corpo até atingir a posição . Os valores de e são, respectivamente,
(a) ; .
(b) ; .
(c) ; .
(d) ; .
(e) ; .
Passo 1
Mola não-linear...

Calma, sem desespero.
As molas lineares tem uma expressão para a força que sempre segue a relação , ou seja quanto maior a deformação, maior é a força da mola proporcionalmente.
A questão fala que a mola é não linear, mas dá pra gente a expressão da força da mola em função da deformação , .
Se a gente substituir os valores de e , ficamos com:
Queremos saber tanto a compressão máxima da mola quanto o trabalho que ela realiza num corpo desde à posição sem deformação .
Passo 2
Primeiro, vamos descobrir a compressão máxima da mola.
Pra você entender melhor, dá uma olhada no gráfico da força da mola (vertical) pela deformação (horizontal).
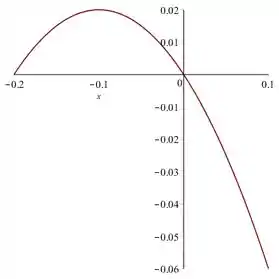
Em , a mola está em seu estado normal (sem deformação).
Quando é negativo significa que ela comprime, já um positivo significa que ela distende.
Como o enunciado fala de compressão, vamos focar na parte de negativo:
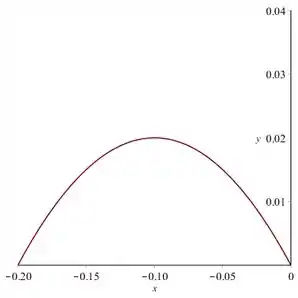
Tá vendo que existe um ponto alí onde a força é máxima? Se continuarmos comprimindo a mola, essa força diminui, certo?
Podemos pensar que a partir desse ponto, a mola para de funcionar da maneira que ela deveria. Ou seja, provelmente, houve uma certa deformação permanente.
Então, vamos considerar que aquele ponto de força máxima é o ponto de compressão máxima.
Como achamos esse ponto de máximo da parábola?
Podemos fazer isso derivando a função e igualando a zero. Pois o ponto de inclinação nula ( vai ser esse vértice da parábola.
Em :
Então, o ponto de compressão máxima vai ser em .
Passo 3
Agora que já sabemos , vamos calcular o trabalho em um corpo, desse ponto até .
Como a força varia ao longo do movimento, não vai ter como fugir. Temos que usar a famosa integral e somar cada trabalhozinho da força em cada deslocamentozinho :
E já sabemos que o trajeto vai de até . Então, os limites de integração ficam:
Assim, achamos o trabalho e . Logo, a alternativa correta é (a).
Resposta
Letra (a)