(Capítulo 7.8 – Exercício 37) A Fig. 7-39 mostra a aceleração de uma partícula de sob a ação de uma força que desloca a partícula ao longo de um eixo , a partir do repouso, de a . A escala vertical do gráfico é definida por . Qual é o trabalho realizado pela força sobre a partícula até a partícula atingir o ponto (a) , (b) e (c) ? Quais são o módulo e o sentido da velocidade da partícula quando ela atinge o ponto (d) , (e) e (f) ?
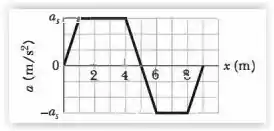
Passo 1
Oi, galerinha! Tudo bom?
Antes de mais nada precisamos lembrar que
Então para encontrarmos o trabalho quando temos um gráfico, basta calcular a área... MASSSSS, precisa ser um gráfico de .
Contudo o que temos aqui é um gráfico de . Mas lembra que
Então precisaremos multiplicar pela massa (, que teremos a força. Beleza?
Ou seja, Basta calcular a área de gráfico correspondente ao deslocamento transformando a aceleração em força. Olha só:
Ou seja, a escala vertical do nosso gráfico agora é dada por !!
Show de bola?!
Passo 2
a) Para acharmos o trabalho realizado pela força de até, basta acharmos a área sob o gráfico nesse intervalo . Somamos a área triangular do gráfico, de a , com a área retangular, de até .
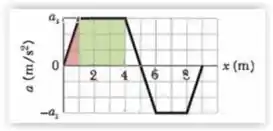
Temos assim,
Entre a
Entre até
O resultado é .
Passo 3
b) Utilizaremos um raciocínio análogo ao do item anterior: obtemos o trabalho realizado pelaforça de até somando as áreas de a e considerando as áreas abaixo do eixo como negativas, sendo assim:
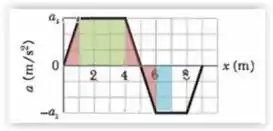
Entre e temos a área calculada anteriomente. Entre e , temos
Entre e temos
Entre e temos
Somando tudo, teremos
obtemos que .
Passo 4
c) Da mesma forma que nos itens anteriores, somando as áreas de a ,
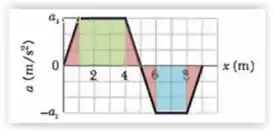
Considerando as áreas abaixo do eixo como negativas, obtemos
Passo 5
d) Bom galera, para encontrar o módulo e o sentido da velocidade da partícula quando ela atinge o ponto usaremos
Assim,
Substituindo os valores,
Logo,
Voltando ao gráfico original, da aceleração em função do deslocamento, vemos que a partícula partiu do repouso e foi acelerada apenas no sentido positivo do eixo;
Assim, em , o vetor velocidade aponta no sentido positivo do eixo.
Passo 6
e) Utilizando o mesmo raciocínio do passo anterior, conseguimos calcular a velocidade para .
Embora a partícula tenha sofrido uma desaceleração a partir do ponto, o vetor velocidade continua a apontar no sentido positivo do eixo .
Passo 7
f) Finalmente, com o mesmo raciocínio anterior, achamos que para .
Embora a partícula tenha sofrido uma desaceleração ainda maior, o vetor velocidade continua a apontar no sentido positivo do eixo .
Resposta
- , sentido positivo do eixo
- , sentido positivo do eixo
- , sentido positivo do eixo