Um bloco ( é arrastado sobre um plano horizontal e seu movimento é estudado durante o deslocamento desde até , com . Uma força é aplicada fazendo um ângulo em relação à horizontal. Considere .
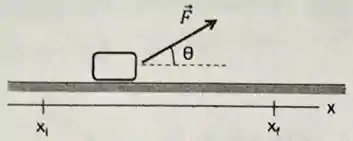
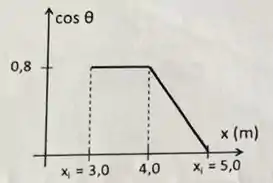
Considere que o módulo de tem valor constante e igual a durante o deslocamento de até , mas suponha que o ângulo varia com a posição de acordo com o gráfico abaixo. Construa o gráfico de como função de , e com base nisto calcule o trabalho realizado pela força ao longo de todo o deslocamento.
Passo 1
Para determinar o gráfico de por, devemos apenas reproduzir o gráfico do só que multiplicado pela força, ou seja multiplicar por . Se liga!
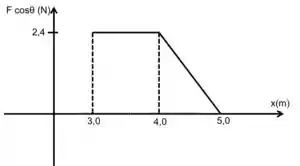
Para determinar o trabalho realizado pela força, basta calcular a área sob a curva:
Resposta
Exercícios de Livros Relacionados
Um bloco de 5,0k g se move em uma linha reta sobre uma superfície horizontal sem atrito sob a influência de uma força que varia com a posição, como mostra a Fig. 7-38. A escala vertical do gráfico é d
Uma força F=c x -3,00 x 2 i → , onde F está em newtons, x em metros e e é uma constante, age sobre uma partícula que se desloca ao longo de um eixo x . Em x= 0 , a energia cinética da partícula é 20,0
Uma única força atua sobre um objeto de 3,0k g que se comporta como uma partícula, de tal forma que a posição do objeto em função do tempo é dada por x=3,0 t - 4,0 t 2+1,0 t 3 , com x em metros e t em
60. Uma partícula de massa m parte de x 0 = 0m com v 00m / s . Ao se mover para a direita sobre o eixo x , a partícula experimenta uma força variável dada por F x = F 0 sen ( c x ) , onde F 0 e c sã
Uma força de 160N estica 0,050m uma certa mola a partir do seu comprimento sem deformação. a) Qual é a força necessária para esticar essa mola 0,015m a partir do seu comprimento sem deformação? E para