A única força horizontal que age sobre uma partícula de 2,0 kg movendo-se na direção é representada na figura abaixo. Na posição a partícula tem velocidade no sentindo positivo do eixo x.
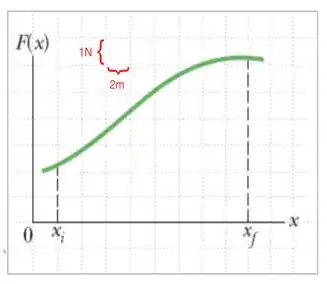
a) Qual o trabalho realizado pela força para mover a partícula de a ?
b) Qual a velocidade da partícula na posição ?
c) Considere que após a posição a força deixa de agir na partícula e a superfície torna-se áspera. Os coeficientes de atrito estático e cinético da superfície são e . Calcule a força de atrito que age sobre a partícula.
d) Qual é a velocidade da partícula em ?
Passo 1
a) Vamos começar!
Bem! Nesse primeiro item, temos que descobrir o trabalho realizado pela força para mover a partícula de a !
Um bom jeito de se obter o trabalho de uma força quando se tem um gráfico, é calcular a área da força sobre o gráfico! Só que a gente nem sabe quanto vale essa força ou qual a expressão pra ela!
Outra forma de descobrir isso, é usando o teorema trabalho energia cinética. Basicamente, ele diz que...
Mas a gente não tem ! Então, vamo ter que tirar um coelho da cartola pra resolver essa letra aqui!
Que tal a gente usar uma série de retângulos pra tentar aproximar a área da força no gráfico! Mais ou menos nesse naipe aqui...
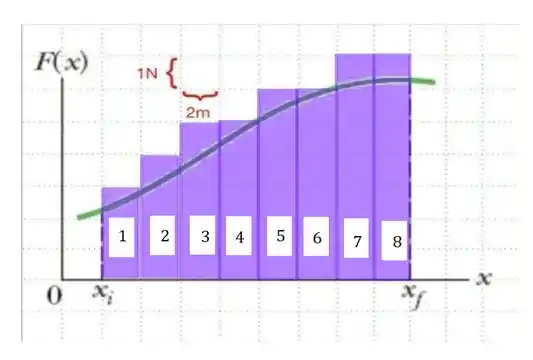
Epa! Aí sim! Com isso, a gente já é capaz de determinar o trabalho da força !
Ele vai ser dado por...
b) E pelo teorema do trabalho energia cinética, podemos determinar a velocidade da partícula na posição final ...
Passo 2
c) Bora pro próximo item!
Se liga! Quando a força para de agir em ela vale aproximadamente uns !
Com os coeficientes de atrito que nós temos, as forças de atrito cinético e estático vão ser iguais à...
Ou seja! Podemos ver que as duas forças são maiores que a força agindo sobre o bloco!
Só que como a força parou de agir sobre o bloco e ele já tá com uma determinada velocidade, então é preferível optar pelo força de atrito cinético.
Passo 3
d) Por último, falta ver a velocidade do bloco em !
Quando a força para de agir sobre o bloco em , ele vai estar exposto a uma aceleração que vai retardar seu movimento! E essa aceleração vale...
Assim, basta aplicar a equação de Torricelli, que podemos obter a velocidade quando :
Onde é o espaço percorrido pela partícula, que no caso vai valer...
Logo;
Resposta
a)
b)
c)
d)