Sejam e .
- Esboçe separadamente as curvas de nível de e .
- Considere a função . Determine o Domínio de .
- É possível estender a função a uma função : , de modo que seja contínua?
- Caso a função do item anterior exista, ela é diferenciável ?
Passo 1
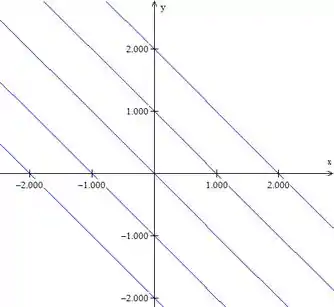
- Vamos começar encontrando as curvas de nível de . Temos:
- Vamos expressar a função , com
- Temos de encontrar uma extensão que torne a função , com , contínua em todo . Percebemos que é uma função contínua em todo o seu domínio. Agora temos de defini-la em
- Primeiro, vamos estudar a função no intervalo . As derivadas parciais são:
Ajeitando:
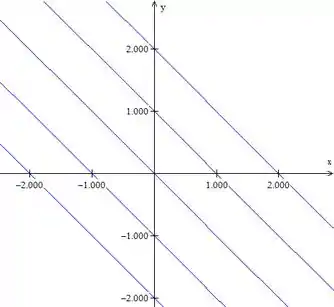
Com . Nota-se que as curvas de nível da função são retas.
Graficamente:
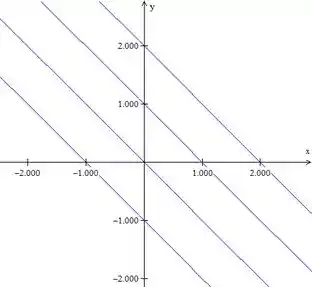
Fazendo o mesmo paraa função , temos:
Com . As curvas de nível da função são retas.
Graficamente:
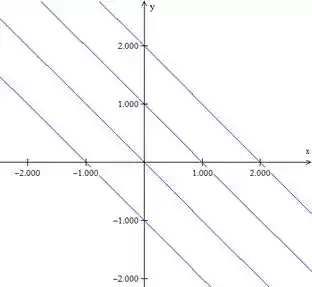
Passo 2
Logo, o dompinio de será:
Passo 3
Vamos lembrar que para uma função ser contínua em um ponto , devemos ter:
Então, vamos calcular esse limite para . Vai ficar:
Logo, definimos a função:
Passo 4
Como as derivadas parciais são contínuas, vamos ter a função diferenciável para todo
Passo 2
Agora, vamos analisar a diferenciabilidade da função quando . Será necessário calcular esse limite, e verificar que seu valor é zero:
Calculando as derivadas parciais pela definição, quando :
Substituindo:
Chegamos a:
Logo, a função é diferenciável em todo
Resposta
- Curvas de nível:
- Sim