1. Como você definiria uma aplicação para uma v.a. que segue um modelo exponencial? Dê um exemplo real onde você recomendaria a utilização deste modelo.

Letra a)

A aplicação da Distribuição Exponencial para caracterizar uma variável aleatória vai ser válida toda vez que a função de probabilidade da nossa v.a. tiver essa cara:

Onde vai ser sempre uma constante positiva. Ou seja, nossa função de probabilidade vai ter sempre um aspecto de função exponencial decrescendo!

Então uma v.a. que segue uma Exponencial tem sua probabilidade diminuindo exponencialmente à medida que os valores de crescem, tipo assim:

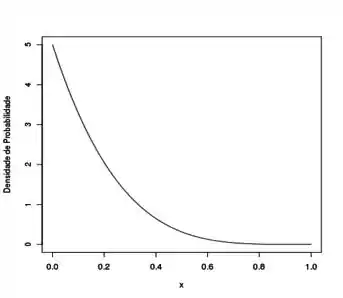
Ela serve para analisar tempos de duração de determinados experimentos, como por exemplo, o tempo de vida útil de um material!