UTFPR, Pato Branco, Cálculo Diferencial e Integral 1, AVs - Pré-Cálculo - AV2 - 2023.1
Calcule o valor de , sabendo que e que .
Passo 1
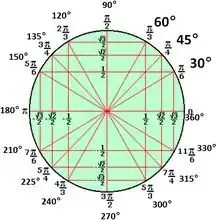
Olá pessoal, para resolver essa questão iremos utilizar do círculo trigonométrico e de uma identidade trigonométrica.
Passo 2
A identidade trigonométrica que nos irá ajudar diz,
Como o ângulo está entre e então nosso cosseno é negativo,
Resposta
Exercícios de Livros Relacionados
Para cada diagrama de dispersão, decida qual tipo de função você escolheria como um modelo para os dados. Explique sua escolha
Resolva a equação sin (x + (pi)/(4)) - sin (x - (pi)/(4)) = sqrt(2)
Resolva as seguintes equações para x ϵ R : a) sen^4 x + cos^4 x = 5 // 8 b) sen^6 x + cos^6 x = 5 // 8 c) sen^4 x + cos^4 x = 1 // 2 d) sen^6 (x)/(2) + cos^6 (x)/(2) = 7 // 16 e) sen^3 x + cos^3 x = 1
Resolva a equação sen^2 x + sen^4 x + sen^6 x = 3
Resolva no conjunto dos números reais a equação sen 2 x = 1 - cos 2 x