UTFPR, Pato Branco, Cálculo Diferencial e Integral 1, AVs - Pré-Cálculo - AV2 - 2023.1
Esboce o gráfico das funções e . Determine o domínio e sua imagem. Descreva que relação existe entre elas.
Passo 1
Para responder essa questão iremos primeiro desenvolver os gráficos.
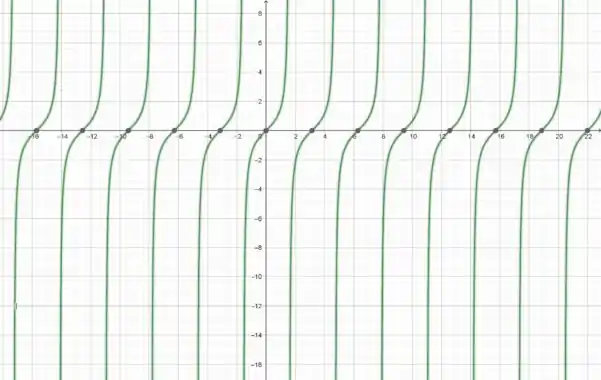
Com ajuda do Geogebra, o gráfico para é,
Passo 2
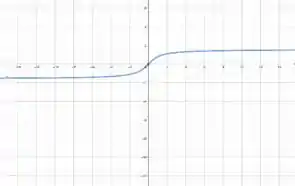
Para o gráfico de , temos
Passo 3
A função f(x)=tan(x) é uma função periódica com período π. É infinita em x=2π+2kπ e x=−2π+2kπ, onde k é qualquer inteiro. A função g(x)=arctan(x) é uma função bijetiva do intervalo (−∞,∞) para o intervalo (−2π,2π). É contínua, diferenciável, e tem uma derivada de 1 em x=0.
O domínio de f(x)=tan(x) é todos os números reais. A imagem de f(x)=tan(x) é o conjunto dos números reais.
O domínio de g(x)=arctan(x) é o intervalo (−∞,∞). A imagem de g(x)=arctan(x) é o intervalo (−2π,2π).
A relação entre f(x)=tan(x) e g(x)=arctan(x) é que g(f(x))=x para todos os números reais x. Em outras palavras, g(x) é a função inversa de f(x).
Resposta
Ver o desenvolvimento.