Calcule o valor da expressão
Passo 1
Nossa querida equação é a seguinte,
O círculo trigonométrico irá nos ajudar bastante nessa,
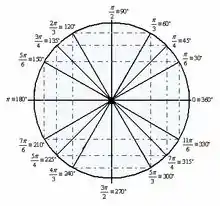
No primeiro e segundo quadrante o valor do seno é positivo, enquanto no primeiro e no quarto quadrante o valor do cosseno é positivo.
Passo 2
E é isso pessoal, espero que tenham entendido e aprendido um pouco mais, um forte abraço e até mais.
Resposta
-1