Um automóvel descreve uma curva compensada que faz um ângulo com a horizontal. A massa do carro é e o raio da curva é dado por . Utilize o número apropriado de algarismos significativos.
Dados:
a) Determine a velocidade necessária para que o carro faça a curva com segurança sem precisar do auxílio do atrito.
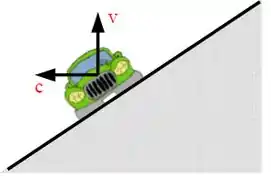
b) Indique no desenho todas as forças que agem no carro quando sua velocidade for igual a . Escreva as equações para o movimento do carro nesta situação usando o sistema de eixos indicado no desenho. O sistema de equações não precisa ser resolvido.
Passo 1
O que está acontecendo quando o carro faz uma curva num plano inclinado?
Bom, a força normal é sempre perpendicular à superfície:
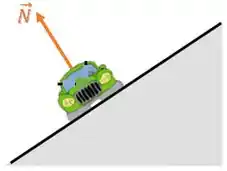
Assim, vai existir uma componente da normal que aponta para o centro da curva:
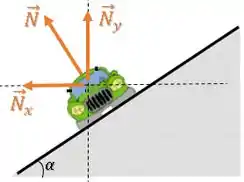
Essa componente atua como força centrípeta.
Passo 2
Mas vamos lá, na letra (a) queremos saber qual a velocidade do carro para que não haja nenhuma força de atrito.
Assim, as únicas forças atuando sobre o carro serão a força normal e a força peso :
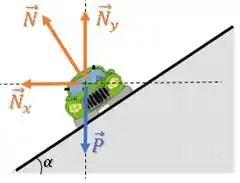
Se essas são as únicas forças e o carro realiza um movimento circular, a força resultante atua como força centrípeta:
E essa força está na horizontal apontando para o centro da curva.
Se não há força resultante na vertical, temos um equilíbrio entre:
Enquanto na horizontal, temos:
Passo 3
Para descobrir as componentes da força normal, vamos utilizar o ângulo de inclinação .
Vamos deslocar o ângulo para o ponto de aplicação da força:
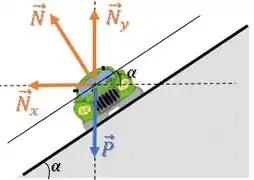
A horizontal e fazem , então aquele ângulo que falta é:
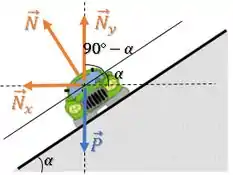
A direção da rampa e também fazem entre si, então aquele ângulo que falta é o próprio :
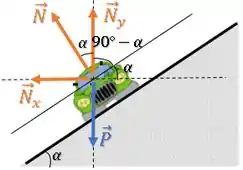
Então, as componentes da força normal são:
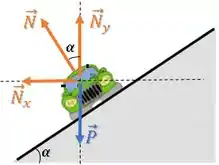
Passo 4
Voltando às equações de forças, temos que na vertical:
Agora, vamos utilizar a equação da força resultante na horizontal:
Passo 5
Ficamos com um sistema assim:
Dividindo a primeira equação pela segunda, temos:
Cortando e , ficamos com:
Queremos descobrir a velocidade , então:
Substituindo os valores:
Passo 6
Na letra (b), agora o carro anda a . Queremos o diagrama de forças e as equações de forças.
Nós vimos que se a velocidade do carro é , não há força de atrito, pois ele apresenta um equilíbrio de forças na vertical.
Porém, se a velocidade for menor que esse valor, o carro tende a deslizar para baixo da curva.
Ué, mas por que?
Quando um carro de corrida entra muito rápido na curva, o que acontece?
Se o carro estiver muuuuito rápido ele tende a deslizar “para fora da curva” ou seja, para cima da rampa.
Se ele estiver muito lento, acontece o efeito contrário e ele tende a deslizar para baixo da rampa.
Passo 7
Como a força de atrito atua contra a tendência de deslizamento do carro, ela estará para cima da rampa:
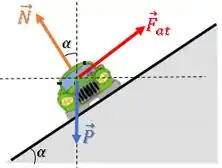
Passo 8
Agora, precisamos escrever as equações de força resultante para essa situação.
Então, vamos voltar com as componente da normal e decompor também nas direções horizontal e vertical:
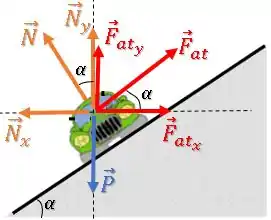
Passo 9
Como o movimento é circular, a força resultante atua como centrípeta e aponta para o centro da trajetória na horizontal.
Assim, temos um equilíbrio na vertical:
Enquanto na horizontal, temos:
Resposta
(a)
(b)
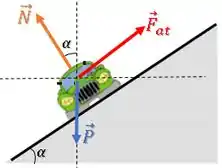
Eixo :
Eixo :