Na figura, as duas partículas, e , ligadas por um fio inextensível e de massa desprezível, descrevem trajetórias circulares concêntricas sobre uma superfície horizontal sem atrito. A partícula está presa por fio, também inextensível e de massa desprezível a um eixo fixo na mesa. Ambas as partículas completam simultaneamente, uma volta a cada segundo e os raios de suas órbitas são e . As massas das partículas são e . Sabendo-se que a tensão no fio entre as partículas e é igual a , qual é a tensão no fio que liga a partícula ao eixo?
A)
B)
C)
D)
E)
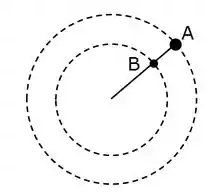
Passo 1
Bom, ele tá querendo a tração no fio que tá entre B e o centro. Vamos fazer um diagrama de forças. Ah, é bom notar que a tração entre A e B vão ter módulos iguais, pois o fio é ideal, e não temos movimento na direção radial.
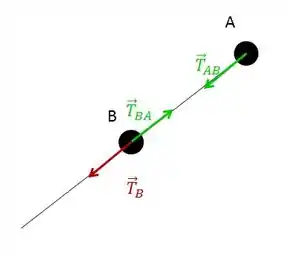
Temos então que:
Olhando para o corpo B:
Bom, a força resultante na direção radial é a força centrípeta:
Então:
Substiuindo os valores:
Agora, temos que descobrir a velocidade de b.
Passo 2
Então, velocidade é o que?
É distância percorrida dividido pelo tempo.
O enunciado fala que o período vale . O período é o tempo necessário para completar 1 volta. E durante uma volta, o corpo percorre uma distância igual ao comprimento da circunferência, que vale .
Então:
Agora, é só substituir:
Que é a nossa letra D!
Resposta
Alternativa D.