Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força Centrípeta

Ver Teoria
Exercício 132123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Força Centrípeta

Um menino está inicialmente em repouso sentado no alto de um monte hemisférico de gelo de raio R . Ele começa a deslizar com uma velocidade inicial tão pequena que pode ser desprezada. Suponha que o atrito com o gelo seja desprezível. Em que altura o menino perde contato com o gelo.

Passo 1

Vamos desenhar essa situação e as forças que estão agindo no menino depois de percorrido um ângulo θ .

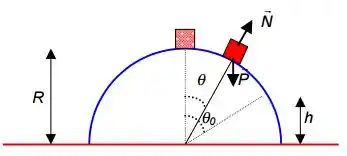
Vamos aplicar a segunda lei de Newton no menino:

P → + N → = m a →

Na aceleração centrípeta vamos ter:

P cos ⁡ θ - N = m a c p

O corpo do menino perde o contato com o hemisfério quando a normal se anular, logo para θ = θ 0 :

N = 0

Logo, teremos que:

P cos ⁡ θ 0 - N = m a c p

m g cos ⁡ θ 0 = m a c p

a c p = g cos ⁡ θ 0

Aplicando a fórmula da aceleração centrípeta teremos:

g cos ⁡ θ 0 = v 0 2 R

Passo 2

Como este sistema é conservativo, a energia mecânica do menino no topo do hemisfério será igual àquela no ângulo θ = θ 0 :

m g R = m g h + 1 2 m v 0 2

Entretanto, sabemos que:

h = R cos ⁡ θ 0

Logo, substituindo isso teremos:

m g R = m g R cos ⁡ θ 0 + 1 2 m v 0 2

v 0 2 = 2 g R 1 - cos ⁡ θ 0

Passo 3

Agora podemos utilizar a equação que encontramos quando a normal é nula:

g cos ⁡ θ 0 = v 0 2 R

g cos ⁡ θ 0 = 2 g R 1 - cos ⁡ θ 0 R

cos ⁡ θ 0 = 2 3

Agora é só substituir na equação da altura:

h = R cos ⁡ θ 0

h = 2 R 3

Resposta

h = 2 R 3

Exercícios de Livros Relacionados

Qual é o menor raio de uma curva sem compensação (plana) que permite que um ciclista a 29k m / h faça a curva sem derrapar se o coeficiente de atrito estático entre os pneus e a pista é 0,32 ?
Em um brinquedo de parque de diversão, um carro se move em uma circunferência vertical na extremidade de urna haste rígida de massa desprezível. O peso do carro com os passageiros é 5,0k N e o raio da
Um estudante que pesa 667N está sentado, com as costas eretas, em uma roda-gigante em movimento. No ponto mais alto, o módulo da força normal F N exercida pelo assento sobre o estudante é 556N . (a) O
Frear ou desviar? A Fig. 6-44 mostra uma vista superior de um carro que se aproxima de um muro. Suponha que o motorista começa a frear quando a distância entre o carro e o muro é d =107m , que a massa
Um bonde antigo dobra urna esquina fazendo uma curva plana com 9,1m de raio a 16k m / h . Qual é o ângulo que as alças de mão penduradas no teto fazem com a vertical?