USP, Sem Campus, Física 1, Coletâneas de Exercícios - Parte I - Cinemática, Leis de Newton, Trabalho e Energia, Questão 64a
Num parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
a) Desprezando o atrito do carrinho com o trilho, qual é o menor valor de necessário para permitir ao carrinho dar a volta completa?
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o menor valor da altura , necessária para permitir que o carrinho der a volta completa no loop de , como mostra a figura:
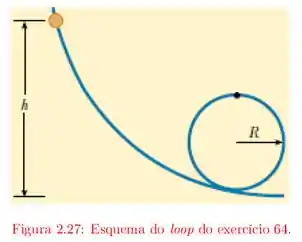
A gente tem que observar o seguinte, quando o carrinho tá no alto da trajetória circular, ele vai tá submetido a duas forças: a normal , que o trilho faz sobre ele, o próprio peso do carrinho. Essas são as forças responsáveis pelo giro e que compõem a força centrípeta:
Se a intenção é achar a altura mínima, buscamos também a velocidade mínima que o carrinho precisa para dar essa volta sem cair. Na situação limite, nossa normal vai ser , que é quando o carrinho estiver perdendo contato com os trilhos (no alto da trajetória circular). Considerando isso e o teorema do trabalho energia, conseguimos chegar em uma expressão para a velocidade e a altura mínima .
Vamos lá!
Passo 2
Vamos começar considerando o caso limite para o qual a força normal é nula e escrever a força centrípeta na forma:
Como a força centrípeta é e a força peso é dada por , temos:
Isolando :
Essa a velocidade mínima para o carrinho dar a volta completa no loop.
Passo 3
Agora, pelo teorema do trabalho e energia potencial, temos:
Onde é o trabalho da força gravitacional (da força peso) e é a variação de energia potencial gravitacional, dada por . Além disso, a gente sabe que a energia potencial pode ser escrita como . No nosso caso, esse na energia inicial e na energia final . Assim, temos:
A gente não sabe quem é , mas a gente sabe que ele pode ser igual a variação da energia cinética (teorema do trabalho e energia cinética). Como inicialmente a velocidade é zero, a variação de energia cinética vai ser dada por:
E a gente viu no passo anterior que , então, substituindo fica:
Como , pelo teorema, vamos ter:
Simplificando dos dois lados:
Logo, a altura mínima será:
Valeu, galera! Até a próxima! 😉