Num parque de diversões, um carrinho desce de uma altura , a partir do repouso, para dar a volta no loop de raio indicado na figura .
b) Se o carrinho cai no trilho em um ponto rotulado por , quando ainda falta percorrer mais um ângulo para chegar até o topo . Calcule .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar o valor do ângulo , quando o carrinho tá no ponto :
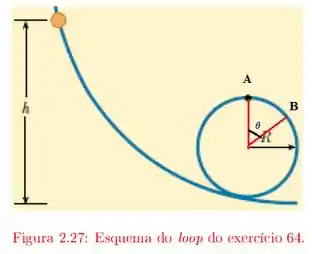
A gente tem que observar o seguinte, para o bloco perder o contato com a superfície, sua velocidade no bloco não precisa ser zero, apenas a normal à superfície (). Assim, vamos ter:
Pra descobrir quem é o peso no ponto , a gente tem que encontrar a componente radial de naquele ponto, usando o ângulo . Com isso a gente encontra a velocidade no ponto e com a velocidade, a gente encontra a energia cinética naquele ponto. A partir daí, basta a gente igualar a energia mecânica no ponto à energia mecânica inicial, já que a energia se conserva, e encontrar uma expressão para o ângulo .
Vamos lá!
Passo 2
Vamos começar considerando o caso limite para o qual a força normal é nula e escrever a força centrípeta na forma:
A força centrípeta é . Mas a força peso vai ser dada por sua componente radial em , que é . Assim, temos:
Isolando :
Essa é a velocidade do carrinho no ponto .
Passo 3
Nós vamos calcular a energia mecânica no ponto e igualar a energia mecânica inicial, já que a energia do movimento se conserva. Mas antes a gente precisa encontrar a altura do ponto .
De acordo com o esquema:
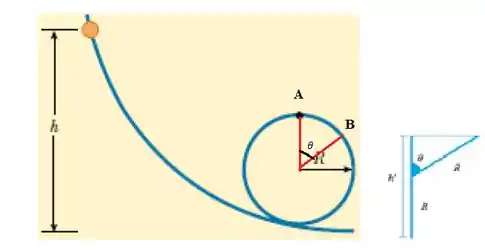
Nós temos:
Passo 4
Bom, agora usando a conservação de energia mecânica, temos:
A energia mecânica no ponto inicial da trajetória é apenas a energia potencial, , porque o carrinho ainda não tava se movendo. No ponto , nós temos energia potencial e energia cinética, a parcela de energia mecânica vai ser dada por e a da energia cinética vai ser dada por . Então, vamos ter:
A gente viu no passo que e viu no passo , que . Então, temos:
Simplificando dos dois lados:
Isolando o :
Então, nosso ângulo é:
Valeu, galera! Até a próxima! 😉