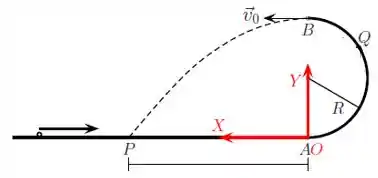
Uma partícula se move sobre uma calha horizontal lisa com velocidade constante de módulo desconhecida. A calha horizontal transforma-se, suavemente, a partir do ponto A, em uma calha semicircular de raio R, tal como indicado na figura. Após percorrer toda a calha semicircular, a partícula deixa a calha no ponto B, que se encontra exatamente acima do ponto A, com velocidade horizontal de módulo v0 e cai de volta na calha horizontal em um ponto P. As calhas estão orientadas de modo que todo o movimento da partícula se passa num mesmo plano vertical. Considere desprezível o atrito entre a partícula e as calha em todos os momentos (entre os pontos A e B). Considere como dados do problema , e a aceleração da gravidade .
d) Determine o módulo da força que a calha semicircular exerce sobre a partícula quando essa passa pelo ponto B.
e) A partícula possui velocidade de módulo igual, maior ou menor que ao passar pelo ponto Q? Justifique claramente sua resposta.
Passo 1
Na letra (d), queremos o módulo da força normal no ponto .
Nesse ponto, temos a força peso apontando para baixo e temos a força normal perpendicular à calha, ou seja, também apontando para baixo:
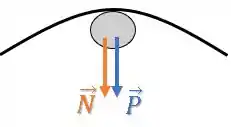
Como a partícula está realizando uma trajetória circular, a força resultante sobre ela deve atuar como força centrípeta:
Passo 2
A velocidade da partícula no ponto é e o raio da trajetória circular é :
Pronto, achamos a força que a calha exerce sobre a partícula.
Passo 3
Na letra (e), queremos saber se no ponto a velocidade é maior, menor ou igual a .
Conforme a partícula vai subindo a calha, a força normal está sempre perpendicular a sua velocidade, então ela não altera seu módulo.
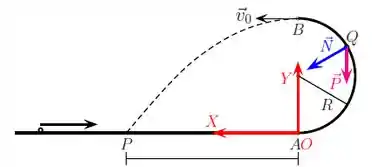
Em contrapartirda, a força peso aponta para baixo durante todo o movimento. Assim, essa força vai ter uma componente gerando uma aceleração na direção contrária à velocidade, fazendo-a diminuir.
Assim, conforme a partícula vai subindo a calha, sua velocidade vai diminuindo em módulo.
Logo a velocidade no ponto é maior que no ponto ().
Dá pra pensar na vida real também. Quando subimos uma rampa de bicicleta, nossa velocidade vai diminuindo se não estivermos pedalando hahah.
Resposta
(d)
(e) Logo a velocidade no ponto é maior que .