UFRJ – Física 1 – Segunda Chamada – 2022.1
2) Um pêndulo cônico é formado por uma partícula de massa , suspensa por um fio ideal, que faz um ângulo com a vertical e realiza um movimento circular, como mostra a figura. Considere o módulo da aceleração da gravidade.
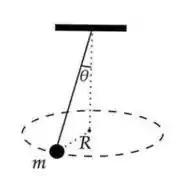
Sabendo que a velocidade angular de rotação é , o raio do movimento circular descrito pela massa é:
a)
b)
c)
d)
e)
Passo 1
Fala aí, galerinha!! Nesse problema a gente tem um pêndulo cônico descrito por essa figura aqui:
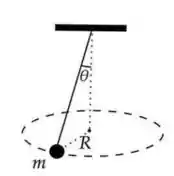
A nossa tarefa é encontrar o raio daquele círculo que a bolinha descreve conhecendo a massa e a velocidade angular, constante, . A ideia aqui é a gente decompor as forças que atuam na bolinha e ver quais que apontam para o centro do círculo.Como temos um movimento circular, sabemos que a força resultando na direção radial é a força centrípeta que é dada por:
E daí a gente vai ver quem é o .Partiiiu!
Passo 2
Vamos começar fazendo a decomposição das forças. Sobre a bolinha somente o peso e a tração estão presentes, beleza?
Nesse problema vale a pena a gente fazer o diagrama de forças de lado. Assim ó:
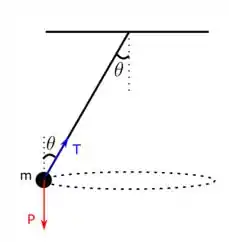
Aqui a gente percebe que podemos fazer uma decomposição da tração:
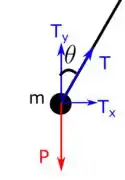
Pela figura temos:
Passo 3
Agora a gente escreve as leis de Newton na direção vertical adotando que para cima é positivo:
E na direção horizontal temos que a única força que atua nessa direção é só que a resultante das forças nessa direção é a força centrípeta, certo? Então temos:
Usando que e :
Isolando ficamos com:
E aí resolvemos essa 😊 Vamos para a próxima??
Resposta
c)