Faça o gráfico das funções e , para .
Passo 1
Oiie, tudo bem?
Aqui temos um trabalho bastante braçal, precisamos fazer o esboço dos gráficos para funções da forma e , em que pode tomar valores dentro do conjunto . Como ainda estamos em pré cálculo, não podemos usar as técnicas usuais de derivada, portanto, teremos que aplicar cada função em alguns pontos e ligá-los. Vamos fazer isso!
Passo 2
Para , temos as funções e , já que . Vamos jogar 5 valores negativos e positivos, formando a seguinte tabelinha
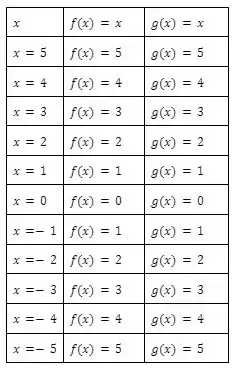
Resultando no gráfico abaixo
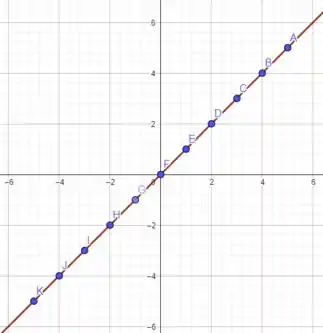
Como as funções são idênticas, os gráficos estão superpostos! Vamos para as próximas funções!
Passo 3
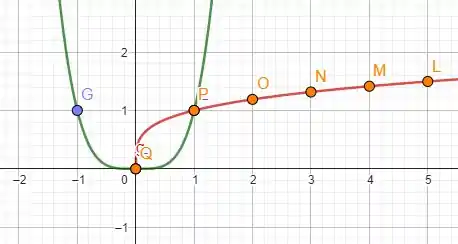
Agora para , temos as funções e . Novamente, jogando valores temos que
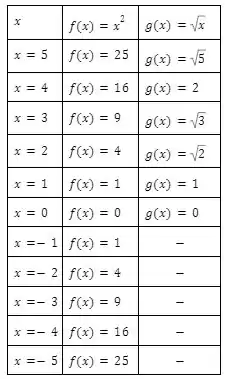
o gráfico toma então a forma
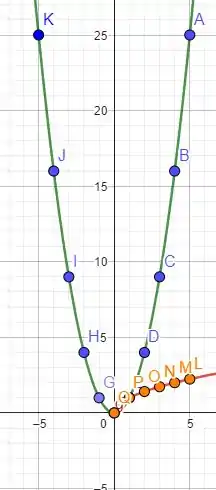
Vamos continuar fazendo isso para todos os ! Bora lá!
Passo 4
Para , temos e , a tabela fica como

e, o gráfico é melhor dividido em duas imagens devido a escala, temos que
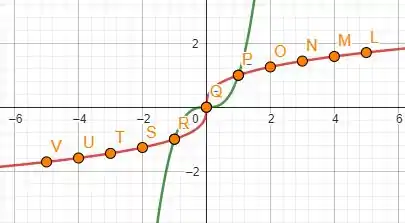
para em evidência, e para temos que
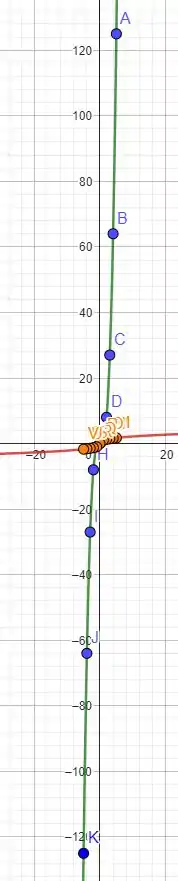
o gráfico de ficará cada vez mais inclinado! Vamos fazer os dois que faltam agora!
Passo 5
Para , temos que

Temos os seguintes gráficos
Agora a escala é tão absurda que os gráficos em escala maior não são sequer relevantes! A tabela te dará informações melhores! Vamos para o último par!
Passo 6
Para temos que e que , temos então

os gráficos são os seguintes
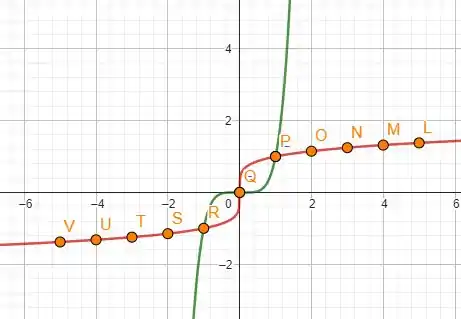
A questão foi isso! te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!