Listas de Cálculo 3 - Profº Edson Figueiredo de Cálculo Diferencial e Integral III da UFPB - 1ª Lista

Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso

1) , a região determinada pelas curvas e .

Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso

2 - , a região do primeiro quadrante dada por

Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso

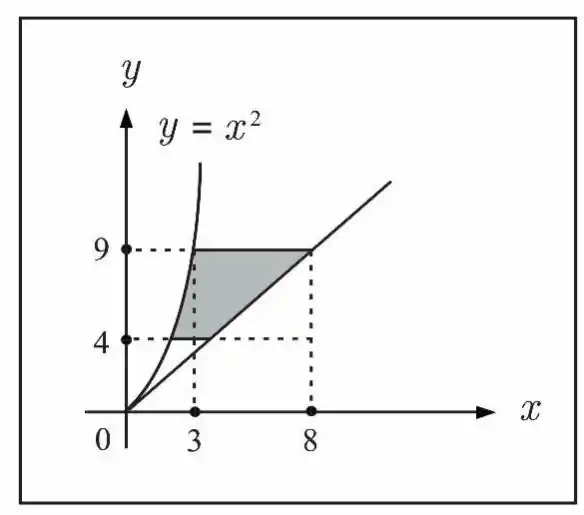
03. , a região do primeiro quadrante definida por , .

04. , a região do primeiro quadrante, limitada pela reta e pelo arco da circunferência de raio , com centro no ponto .

Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso

05. , o triângulo com vértices nos pontos , e .

Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso

06. , a região retangular definida pelas desigualdades ,

Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso

07. , limitada pela parábola e pelas retas e .

Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso

08. , a região definida por , .

Nos exercícios 09 a 12, escreva as integrais dadas com a ordem de integração invertida

9.

Nos exercícios 09 a 12, escreva as integrais dadas com a ordem de integração invertida

10.

Nos exercícios 09 a 12, escreva as integrais dadas com a ordem de integração invertida

11.

Nos exercícios 09 a 12, escreva as integrais dadas com a ordem de integração invertida

12.

13. Escreva

como uma integral dupla e esboce graficamente a região de integração correspondente.

14. Calcule , sendo . (Sugestão: Faça e )

Calcule , onde

(Sugestão: Faça e )

Se , mostre que .

(Sugestão: Faça e )

Calcule a área da região que não contém a origem, sendo limitada pela rela e pela circunferência .

Calcule a área da região interior à elipse de equação .

Calcule a área da região compreendida entre as parábolas e .

Calcule a área da região em destaque na figura abaixo.

Calcule a área comum aos círculos limitados por e .

Calcule a área da região interior à lemniscata e exterior à circunferência de centro na origem e raio unitário.

Calcule a área da região interior ao cardióide e à direita da reta .

Calcule o volume limitado pelo cilindro e pelos planos e .

Calcule o volume limitado pelo parabolóide , pelo plano e pelos cilindros e .

Calcule o volume limitado pelo parabolóide , pelo cilindro e pelo plano .

Calcule o volume do sólido limitado pelo plano , pelo cilindro e pelo cone .

Calcule o volume do sólido contido no parabolóide , limitado por este e pela esfera de equação .

Calcule o volume do sólido do primeiro octante, limitado pelas superfícies , , , , e .

(Sugestão: Faça e )

Ao calcular-se, por dupla integração, o volume do sólido situado abaixo da superfície de equação e acima de uma região do plano , obteve-se a seguinte soma de integrais

Qual é esse sólido? É possível obter o valor do mesmo volume sem a necessidade do cálculo de uma soma de integrais? Qual o valor do volume?