UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 25
Calcule o volume limitado pelo parabolóide , pelo plano e pelos cilindros e .
Passo 1
Eaew, belezinha?
Temos que calcular o volume limitado pelo parabolóide
acima do plano . E, delimitado lateralmente pelos cilindros parabólicos
e
Este sólido é tal que
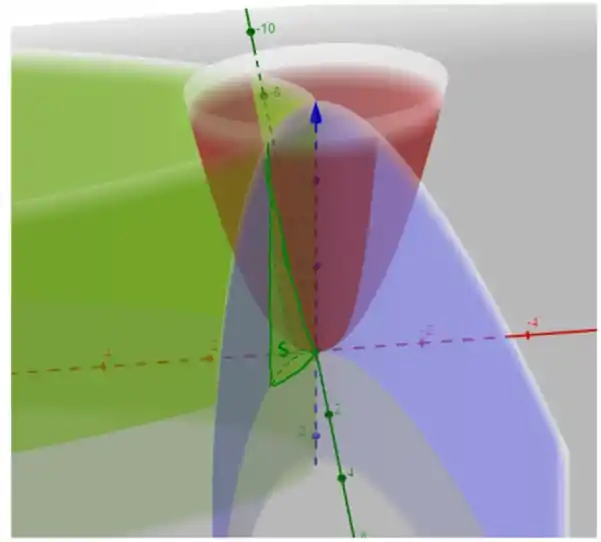
note que as laterais são os cilindro, a base é o plano e a tampa é o parabolóide , o volume pode ser calculado usando
em que . Vamos escrever a nossa função e reescrever a região , estabelecendo assim limites de integração! Saca só!
Passo 2
A função é dada pelo parabolóide que serve como tampa, temos que
A região é delimitada pelos cilindros parabólicos, a região pode ser visualizada como
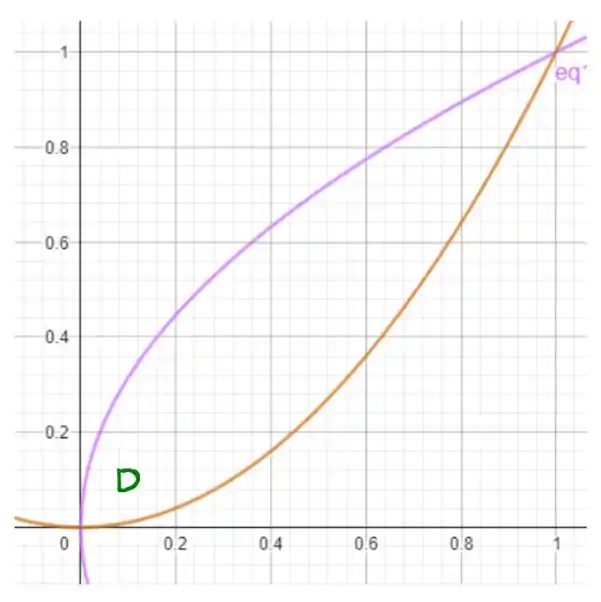
Note que a interseção acontece nos pontos e . Com oa região não é retangular, precisamos escolher uma ordem de integração. Vamos escolher trabalhar com indo de até , e partindo de (parábola inferior) até que é a parábola superior. Ou seja, nossa integral se torna
Ou seja, como os limites de dependem de , precisamos primeiro integrar em ! Vamos fazer isso!
Passo 3
Temos que resolver
integrando primeiro em , temos que
e, também que
usando estes resultados em nosso volume, temos que
distribuindo temos que
Vamos resolver essas integrais agora!
Passo 4
Todas as integrais podem ser obtidas diretamente como
Portanto, o volume é dado por
Em que fiz o MMC para conseguir somar estes termos (tenha paciência que você consegue!). A questão foi isso! Te vejo na próxima! Tchau Tchau!