UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 28
Calcule o volume do sólido contido no parabolóide , limitado por este e pela esfera de equação .
Passo 1
Eaew, belezinha?
Temos que calcular o volume contido no parabolóide
e limitado pela esfera
Este sólido é tal que
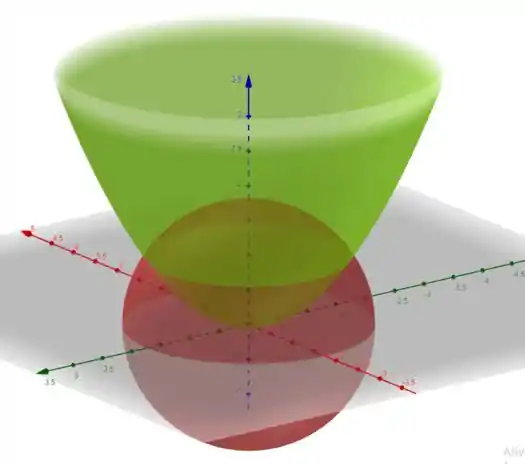
note que a tampa é a esfera e a base é o parabolóide, o volume deve ser calculado usando que
Vamos procurar os limites e integração adequados ao nosso problema! Saca só!
Passo 2
Vamos resolver este problema usando coordenadas cilíndricas da forma
, e
nessas condições as equações tomam a forma
e, também
como o jacobiano de coordenadas cilíndricas é dado por
O nosso volume é então dado por
Vamos procurar os limites de integração!
Passo 3
A interseção entre as superfícies resulta em
Aplicando bhaskara encontramos a seguinte solução
resultando nas duas raízes
e
a raíz negativa não é solução para a equação do parabolóide, portanto, temos que apenas a raíz positiva é válida. A interseção com o plano , resulta em uma circunferência
e, portanto, a integral de volume se torna
Os limites não são constantes, portanto, temos que integrar primeiro na variável cujo limites depende das outras, ou seja, integrar primeiro em . Vamos lá!
Passo 4
A integral em pode ser identificada diretamente como
ou seja, nosso volume é dado por
dividindo em duas integrais temos que
A integral em no segundo termo pode ser identificada como
e, para a outra precisando fazer uma substituição simples da forma
e
de forma que a integral se torna
essa integral resulta em
que pode ser simplificado como
O volume é então dado por
com a integral em é simplesmente
finalmente obtemos
A questão foi isso! Te vejo na próxima! Tchau Tchau!