UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 1
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
1) , a região determinada pelas curvas e .
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema, queremos obter a integral da função aplicada na região , onde é a região definida entre e .
E aí, tem ideia do que fazer? 🤔
O segredo é conseguir definir a região como os limites de integração de
Se conseguirmos fazer isso, a primeira integral deve ser definida entre duas funções e a última integral deve ser definida entre duas constantes.
Bora começar! 😁
Passo 2
Vamos começar esboçando a região .
Esboçando a reta e a parábola .
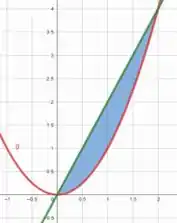
Percebemos que a região em azul (a região ) é limitada superiormente entre a reta e inferiormente pela parábola .
Dessa forma, podemos definir que varia entre o intervalo
E a região é definida em nos pontos onde a reta e a parábola se cruzam, ou seja, e .
Tranquilo até aqui? 😉
Passo 3
Montando nossa integral com base no que nos dados que obtivemos...
Integrando com relação a , temos
Aplicando os limites de integração
Integrando o resultado com relação a
Aplicando os limites de integração em
Fim! Iae, o que achou? Responde Aí! 😁
