UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 20
Calcule a área da região em destaque na figura abaixo.
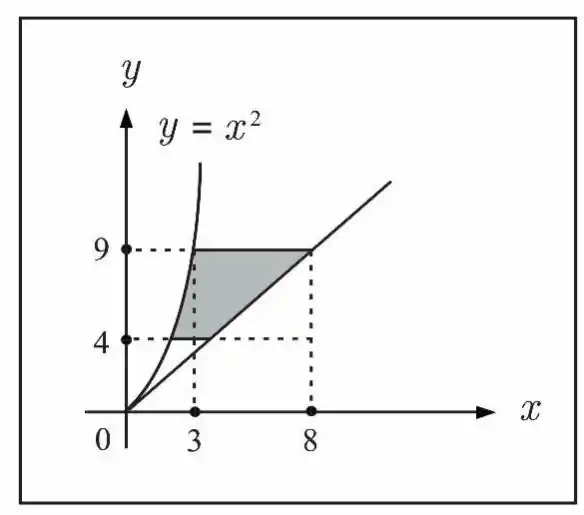
Passo 1
Oiie, tudo bem?
Precisamos calcular a área da seguinte região
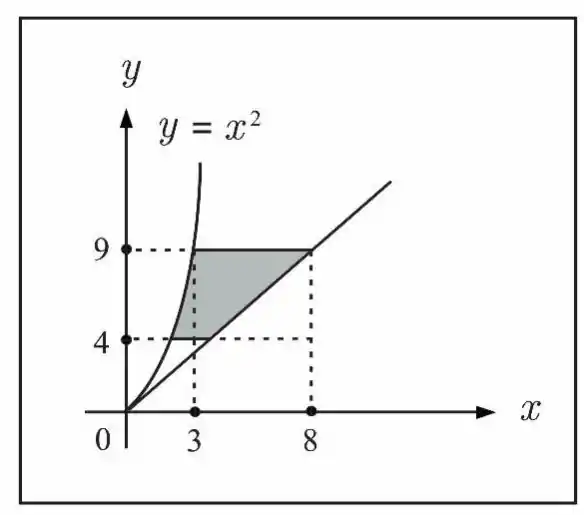
O cálculo da área pode ser feito utilizando integração dupla como
Ou seja, é apenas o trabalho de calcular os limites de integração! Neste caso é uma escolha do que integrar primeiro sem precisar de mudanças de coordenadas! Saca só!
Passo 2
Note que temos que a variável vai da parábola (note que estamos em valores positivos de ) até uma reta, a equação da reta pode ser obtida utilizando as informações da imagem, temos que a reta passa pela origem, e também que
portanto, podemos identificar uma equação de reta como
desta forma, temos que a variável obedece o intervalo
e a variável está entre as constantes
A integral se torna então
Como a região não é retangular, a ordem de integração importa, e devemos resolver primeiro a integral em , pois seus limites dependem de ! Bora lá!
Passo 3
Temos que a integral em é da forma
De forma que a área será dada por
ela pode ser separada em duas integrais da forma
Essas integrais podem ser identificadas como
e, analogamente
E, finalmente, a área pode ser escrita como
ou simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!