UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 17
Calcule a área da região que não contém a origem, sendo limitada pela rela e pela circunferência .
Passo 1
Eaew, belezinha?
Temos que calcular a área da região delimitada pela reta e a circunferência (escolhendo o pedaço que não contém a origem), a região é a seguinte
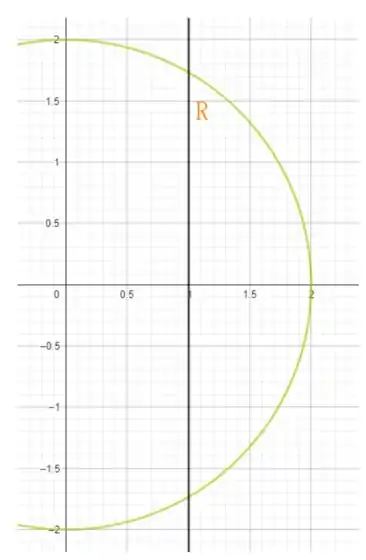
O cálculo da área pode ser feito utilizando integração dupla como
Ou seja, é apenas o trabalho de calcular os limites de integração! Vamos procurar uma maneira conveniente de fazer isso! Aqui é interessante utilizar coordenadas polares para reescrever nosso problema, mesmo que possa ser feito diretamente! Saca só!
Passo 2
Usando que
e
e o jacobiano em coordenadas polares que é conhecido como
podemos escrever a integral como
Para encontrar os limites de integração, precisamos reescrever a nossa região em coordenadas polares. Note que quando , temos que
e, portanto
e o valor máximo do raio é simplesmente o raio da circunferência dado por (uma reta constante). A interseção da reta com a circunferência , nos dará os outros limites como
devido a paridade da função cosseno temos dois ângulos que obedecem a equação acima, os resultados são
A região é então representada como
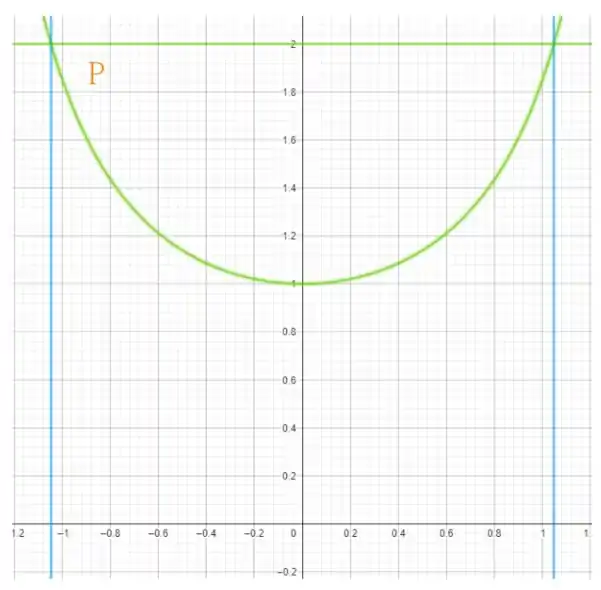
e, portanto, os limites da nova integral são
Como nossa região não é retangular a ordem da integração importa, e devemos integrar primeiro em já que os limites dependem de . Vamos lá!
Passo 3
Vamos começar com a integral em , temos que
podemos identificar que
Temos então que nossa integral se reduz à
Vamos resolver agora a integral que restou!
Passo 4
Temos que resolver
para identificar a segunda integral devemos lembrar que
e, principalmente que
sendo assim, temos que
Avaliando os limites, temos que
A segunda integral é mais simples, podemos identificar diretamente que
E, portanto, a área da região é dada por
A questão foi isso! Te vejo na próxima! Tchau Tchau!