UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 30
Ao calcular-se, por dupla integração, o volume do sólido situado abaixo da superfície de equação e acima de uma região do plano , obteve-se a seguinte soma de integrais
Qual é esse sólido? É possível obter o valor do mesmo volume sem a necessidade do cálculo de uma soma de integrais? Qual o valor do volume?
Passo 1
Eaew, tudo certo contigo?
O enunciado indica que ao tentar calcular o volume de um sólido por integração dupla, encontraram a seguinte soma de integrais
em que o sólido tem como tampa a superfície delimitada por uma região . O objetivo aqui é visualizar o sólido através desta soma de integrais, e então verificar se é possível escrevê-la como uma única integral, e resolvê-la! Para começar precisamos analisar estes limites de integração! Saca só!
Passo 2
Temos que a primeira integral na soma nos indica uma região que não é retangular (os limites não são constantes), temos que está no intervalo a , mas vai de zero até a reta
da mesma forma para a segunda integral, temos que está no intervalo constante a e vai de até a reta
Isso nos indica a seguinte região
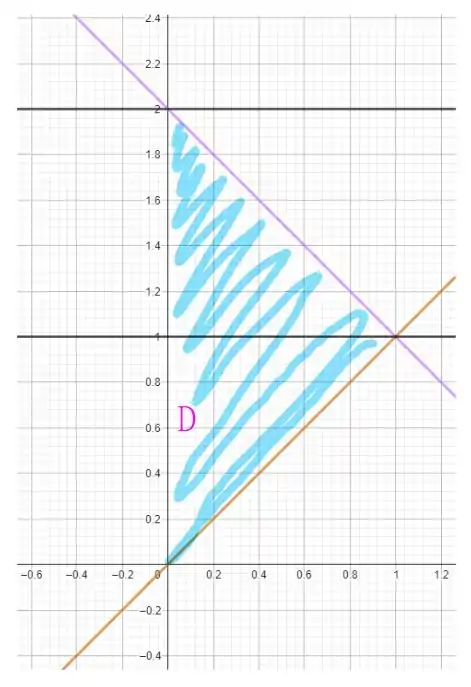
ou seja, nosso sólido é a parte do parabolóide entre os planos e , limitados lateralmente pelos planos , e . Podemos escrever esse problema como uma única integral dupla? Vamos verificar!
Passo 3
Podemos se integrarmos primeiramente em com os limites
o resultado é o mesmo! Integrando primeiramente em , temos que
Temos que
e, também que
O volume se torna
Vamos integrar em agora!
Passo 4
Podemos dividir tudo em quatro integrais da forma
podemos identificar que
e, que
Para a integral que falta é conveniente fazer a mudança
e
de forma que temos
que é simplesmente
O volume então é dado por
A questão foi isso! Te vejo na próxima! Tchau Tchau!