Calcule a área da região interior à lemniscata e exterior à circunferência de centro na origem e raio unitário.
Passo 1
Oiie, tudo bem?
Precisamos calcular a área da seguinte região delimitada pela lemniscata
e uma circunferência unitária, a região é tal que
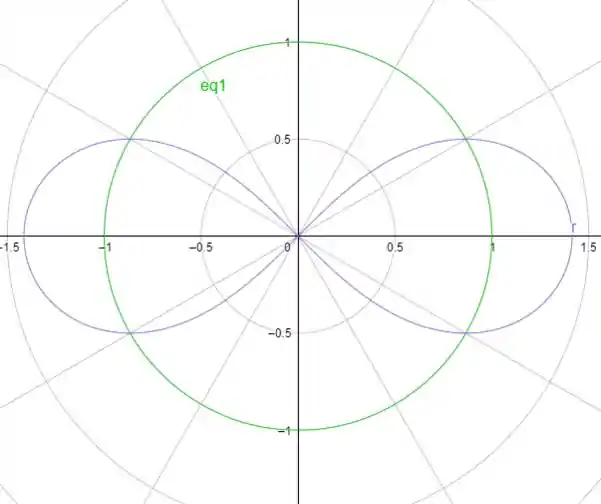
A leminiscata é uma curva que parece o símbolo de infinito! Em coordenadas polares temos que uma circunferência tem equação dada por
a área de curvas polares é calculada usando a seguinte relação
Como aqui temos a área entre duas curvas temos que fazer a diferença entre as áreas para obter apenas o desejado! Para facilitar vamos usar alguns argumentos de simetria! Vem comigo!
Passo 2
Observando nossa figura podemos perceber que devemos retirar a área do círculo da área da lemniscata, apenas tendo cuidado para selecionar o intervalo desejado, em nosso caso, o pedacinho da lemniscata que escapa do círculo em ambas as extremidades (como ambos têm o mesmo tamanho vamos calcular a área para um deles e multiplicar o resultado por dois). O ângulo inicial e final é dado pela interseção da leminscata com o círculo, portanto, da equação e da equação temos que
Portanto, queremos um ângulo tal que
este ângulo é dado por
a área será então
Vamos calcular as integrais agora!
Passo 3
As integrais são da forma
e, também
De forma que nossa área é dada por
ou seja, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!