Exercícios Resolvidos de Inversão da Ordem de Integração – Coordenadas Cartesianas
Ver TeoriaEnunciado
UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 11
Nos exercícios 09 a 12, escreva as integrais dadas com a ordem de integração invertida
11.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema queremos inverter os limites de integração da integral
Tem alguma ideia de como fazer isso? 🤔
Na prática para passar a integral de para temos que olhar para os limites de integração de e de e tentar reescreve-las de modo que invertemos a função ou sendo os limites da última integral sempre definidos entre duas constantes.
Bora ver como é na prática? 😉
Passo 2
Nesse caso, perceba que varia entre duas constantes e . Já está definida entre duas funções e .
Não sabemos qual é o valor de , então podemos definir um valor qualquer só pra podermos visualizar a região. Por exemplo, se , temos
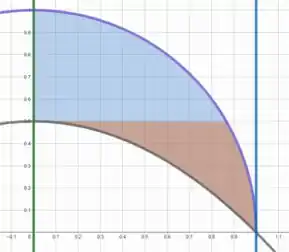
Perceba que os limites horizontais inferiores da região não são os mesmos em todo o espaço, então vamos precisar separar a integral em duas, uma para a parte azul e outra para a parte laranja, quando somadas resulta na região dada inicialmente.
Vamos começar isolando em um lado da equação nos limites de
Substituindo e em , temos
Agora fazemos o mesmo para
Entendeu essa parte? 🤔
Passo 3
Temos três pontos para ... , e
E também três pontos para ... , e .
Assim, começando pela região azul, o limite horizontal em está definito entre as curvas e . Já verticalmente em , a região está definida entre e .
E por último, para a região laranja, os limites horizontais em são dados por e . Já verticalmente em entre e .
Assim, a região total será a soma dessas duas integrais, ou seja.
É isso! Essa resolução te ajudou? Responde Aí! ✌
