UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 18
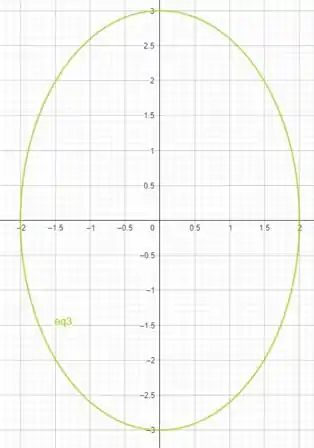
Calcule a área da região interior à elipse de equação .
Passo 1
Eaew, belezinha?
Temos que calcular a área da seguinte elipse
dada por
O cálculo da área pode ser feito utilizando integração dupla como
Ou seja, é apenas o trabalho de calcular os limites de integração! Vamos procurar uma maneira conveniente de fazer isso! Se isso fosse uma circunferência seria bastante simples utilizar coordenadas polares para resolver o problema, no entanto, para uma elipse primeiro precisamos reescrever o sistema em coordenadas em que ela seja vista como uma circunferência! Lembra como fazer isso? Saca só!
Passo 2
A equação da elipse pode ser escrita como
então se usarmos um sistema de referências em que
e
temos que a elipse se torna a seguinte circunferência
Mas, como mudamos o sistema de coordenadas precisamos encontrar o jacobiano dessa mudança através da definição
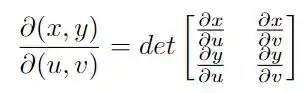
aplicando a definição, temos que
Ou seja, as integrais estão relacionadas por
Como temos agora uma circunferência como região! Podemos calcular a integral usando coordenadas polares diretamente! Bora lá!
Passo 3
Usando que
e
e o jacobiano em coordenadas polares que é conhecido como
podemos escrever a integral como
Como essa é uma circunferência completa de raio , temos que os limites são
Que é uma região retangular (limites constantes), ou seja, podemos integrar em qualquer ordem! Vamos fazer isso!
Passo 4
A integral em é dada por
e, a integral em é
Juntando os resultados, temos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!