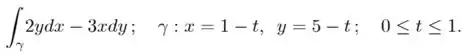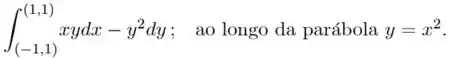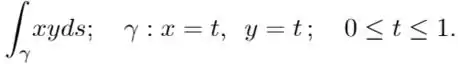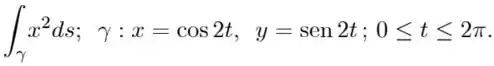Listas de Cálculo de Várias Variáveis de Cálculo Diferencial e Integral III da UFPB - Lista 2 - Integral de Linha

Esboce o gráfico de cada curva abaixo, indicando a orientação positiva.

(a)

Esboce o gráfico de cada curva abaixo, indicando a orientação positiva.

(b)

Esboce o gráfico de cada curva abaixo, indicando a orientação positiva.

(c)

Esboce o gráfico de cada curva abaixo, indicando a orientação positiva.

(d)

Esboce o gráfico de cada curva abaixo, indicando a orientação positiva.

(e)

Esboce o gráfico de cada curva abaixo, indicando a orientação positiva.

(f)

Calcule o comprimento da hélice do exercício (f).

Seja uma função contínua sobre um arco regular de comprimento L. Se , em todos os pontos do arco , mostre que:

Calcule as seguintes integrais de linha ao longo do caminho indicado:

a)

Calcule as seguintes integrais de linha ao longo do caminho indicado:

b)

Calcule as seguintes integrais de linha ao longo do caminho indicado:

e)

Calcule as seguintes integrais de linha ao longo do caminho indicado:

f)

Calcule , nos seguintes casos:

(a) ; é o círculo .

Calcule , nos seguintes casos:

(a) ; é a fronteira da região , orientada no sentido horário.

Calcule , nos seguintes casos:

(c) ; é o segmento de reta da origem ao ponto .

Calcule , nos seguintes casos:

(d) ; é o arco da parábola , e ; .

Calcule , nos seguintes casos:

(e) ; consiste do segmento de reta de a , seguido do seguimento de reta de a .

Sob ação da força , um objeto percorre a elipse , no sentido anti-horário. Qual o trabalho realizado pelo campo ?

Com o auxílio do Teorema de Green, calcule as seguintes integrais de linha:

(a) é um arco simples fechado e regular.

Com o auxílio do Teorema de Green, calcule as seguintes integrais de linha:

(b) é um contorno simples regular e fechado, que não envolve a origem.

Com o auxílio do Teorema de Green, calcule as seguintes integrais de linha:

(c) .

Com o auxílio do Teorema de Green, calcule as seguintes integrais de linha:

(d) é um círculo de raio e e são funções de classe na região delimitada pela curva .

Com o auxílio do Teorema de Green, calcule as seguintes integrais de linha:

(e) é a elipse .

Com o auxílio do Teorema de Green, calcule as seguintes integrais de linha:

(f) é a cardioide , .

Considere e , definidas para e seja a região descrita por . Mostre que:

(a)

Considere e , definidas para e seja a região descrita por . Mostre que:

(b)

Um arame tem o formato da parte da elipse situada no primeiro quadrante e a densidade no ponto é . Qual a massa do arame?

Um arame tem a forma da curva interseção do hemisfério , , com o plano e a densidade no ponto é . Qual a massa do arame?

Seja uma função contínua sobre um arco regular de comprimento . Se , em todos os pontos do arco , mostre que:

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(c) ao longo da rela .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(d) ; .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(g) ; é o triangulo de vértices , e .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(h) ; .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(i) ; ao longo do semicírculo .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(j) ; ao longo da curva , , .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(k) .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(l) .

3. Calcule as seguintes integrais de linha ao longo do caminho indicado:

(m) consiste dos arcos e ,

5. Calcule , onde é a circunferência , percorrida no sentido positivo, e é a circunferência ; percorrida no sentido horário.

6. Calcule ; onde consiste no arco da parábola , ; seguido do segmento de reta que une os pontos e .

7. Na regão ; interior à elipse e exterior à circunferência , com , considere o campo vetorial . Calcular a integral de linha .

As curvas

São percorridas no sentido anti-horário e considere um campo de classe no domínio tal que:

Qual o valor da integral de linha ?

Um arco não regular. Seja o arco dado por: , e . Note que a coordenada do arco é:

Com derivada , para e .

Sendo esta derivada descontínua em , concluímos que o caminho não é regular.