UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 23
Calcule a área da região interior ao cardióide e à direita da reta .
Passo 1
Oiie, tudo bem?
Precisamos calcular a área da seguinte região delimitada pelo cardióide
e a direita da reta , ou seja, temos a seguinte região
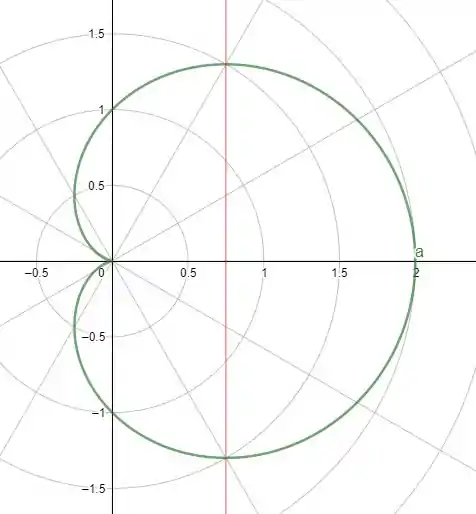
O cardióide é uma curva que parece um coração! Em coordenadas polares, temos que a reta determina apenas um ângulo, já que
a área de curvas polares é calculada usando a seguinte relação
Como aqui temos a área entre duas curvas temos que fazer a diferença entre as áreas para obter apenas o desejado! Vamos tentar encontrar os limites de integração!
Passo 2
A equação nos dá a curva secante
uma vez que , a interseção entre elas ocorre quando
dividindo tudo por , temos que
vamos pensar nisso como um polinômio da forma
Aplicando Bhaskara, temos que
ou seja, temos as raízes
e
como temos que
procuramos ângulos tais que
e
da mesma forma, queremos ângulos tais que
e
a segunda relação acima não existe pois , sendo assim, os ângulos de interseção são dados pela primeira relação, e temos que pela paridade do cosseno, obtemos
Vamos calcular agora a área desejada!
Passo 3
Observando nossa figura podemos perceber que devemos retirar a área a esquerda da reta da área do cardióide, apenas tendo cuidado para selecionar o intervalo desejado. A área será dada por
podemos identificar diretamente algumas integrações como
e, também que
Para a terceira integral vamos usar a relação de meio ângulo para o cosseno, de forma que
ou simplesmente
Falta apenas uma integral! Resumindo o que obtivemos até agora, temos que
Vamos resolver a integral que falta agora!
Passo 4
Para resolver essa integral vamos lembrar que
portanto, podemos garantir que
e, finalmente, podemos escrever a área como
ou simplesmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!