UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 5
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
05. , o triângulo com vértices nos pontos , e .
Passo 1
Como vai meu consagrado? 😁 Bora aprender como resolver essa questão? 😉
Nesse problema, queremos obter a integral da função aplicada na região , onde é a região definida pelo triângulo com vértices nos pontos , e .
E aí, tem ideia do que fazer? 🤔
O segredo é conseguir definir a região como os limites de integração de
Se conseguirmos fazer isso, a primeira integral deve ser definida entre duas funções e a última integral deve ser definida entre duas constantes.
Bora começar! 😁
Passo 2
Vamos começar esboçando a região .
Plotando os pontos e traçando o triangulo, temos
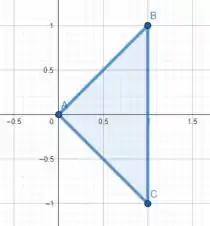
E nosso desafio agora é conseguir descrever a região dentro dos limites de integração de .
Podemos imaginar que os seguimentos e são retas que definem nossa região em .
O seguimento se alongado, vemos que poderá cortar os quadrantes ímpares ao meio e a reta que é capaz de fazer isso é a reta .
Já se alongarmos o seguimento podemos ver que a reta formada cortaria os quadrantes pares ao meio e a reta que faz isso é a reta .
Logo temos que
E pela figura, vemos que varia de a .
Sacou? 😁
Passo 3
Montando a integral com os limites de integração que definimos para e , temos
Integrando em , temos
Aplicando os limites de integração de ...
Como o resultado da primeira integral é , certamente a segunda integral também é , logo
Pegou o esquema? Responde Aí! 😁
