Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 143123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 4

04. f x , y = x , D a região do primeiro quadrante, limitada pela reta x + y = 2 e pelo arco da circunferência de raio 1 , com centro no ponto 0,1 .

Passo 1

Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Nessa questão, temos que obter a integral de f x , y = x aplicado na região D dada entre a reta x + y = 2 e a circunferência de raio 1 centrada em 0,1 .

E aí, tem ideia do que temos que fazer? 😐

Primeiro, vamos visualizar a região de integração D e tentar definir analiticamente essa região em uma integral dupla de f x , y .

Bora começar! 😁

Passo 2

Esboçando a reta x + y = 2 e a circunferência de raio 1 centrada em 0,1 dada pela equação x 2 + y - 1 2 = 1 , temos

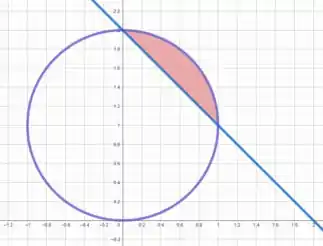
Perceba que descrever essa região em uma integral dupla vai ser muito difícil, porém, podemos transladar nosso sistema para o centro da circunferência.

Pra isso, substituímos todos os y do problema, por y + 1

Assim, a reta passa de x + y = 2 para x + y + 1 = 2 → x + y = 1

E a circunferência de x 2 + y - 1 2 = 1 para x 2 + y + 1 - 1 2 = 1 → x 2 + y 2 = 1

Com essa mudança, a região fica bem mais fácil de ser descrita, olha só

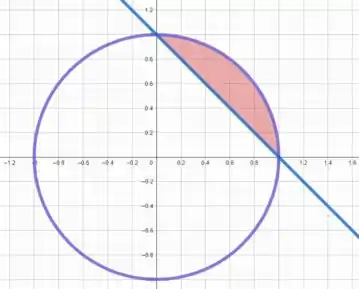
Tudo certo até aqui? 😉

Passo 3

Como temos uma simétrica polar na nossa região, podemos aplicar coordenadas polares no nosso problema, ou seja, fazemos x = r c o s θ e y = r s e n θ . E também, ao invés de integrar em x e y , agora integramos em r e θ .

Para θ é mais fácil de definir os limites de integração, pela descrição da região, vemos que θ varia de 0 a π / 2 .

Porém, r está variando de 1 até a reta x + y = 1 , ou seja

x + y = 1 → r c o s θ + r s e n θ = 1

r c o s θ + s e n θ = 1

r = 1 c o s θ + s e n θ

Ou seja, aplicando esses limites de integração na integral de f lembrando de multiplicar f pelo jacobiano r ...

∫ 0 π 2 ∫ 1 c o s θ + s e n θ 1 r c o s θ r d r d θ

∫ 0 π 2 ∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r d θ

Integrando em r , temos

∫ r 2 cos ⁡ θ d r = r 3 3 cos ⁡ θ

Aplicando os limites de integração...

∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r = 1 3 3 cos ⁡ θ - 1 c o s θ + s e n θ 3 3 cos ⁡ θ

∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r = 1 3 cos ⁡ θ - cos ⁡ θ c o s θ + s e n θ 3

Entendeu essa parte? 😎

Passo 4

Substituindo o resultado na integral, temos

∫ 0 π 2 ∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r d θ

∫ 0 π 2 1 3 cos ⁡ θ - cos ⁡ θ c o s θ + s e n θ 3 d θ

1 3 ∫ 0 π 2 cos ⁡ θ - cos ⁡ θ c o s θ + s e n θ 3 d θ

Vamos separar essa integral em duas partes...

1 3 ∫ 0 π 2 cos ⁡ θ d θ - 1 3 ∫ 0 π 2 cos ⁡ θ c o s θ + s e n θ 3 d θ

Primeiro vamos calcular a integral de cos ⁡ θ

∫ cos ⁡ θ d θ = s e n θ

1 3 ∫ 0 π 2 cos ⁡ θ d θ = 1 3 s e n π 2 - s e n 0

1 3 ∫ 0 π 2 cos ⁡ θ d θ = 1 3

Tranquilo, não é? 👀

Passo 5

Agora vamos calcular a outra integral

1 3 ∫ 0 π 2 cos ⁡ θ c o s θ + s e n θ 3 d θ

Dividindo o numerador e o denominador por s e c 3 θ , temos

1 3 ∫ 0 π 2 cos ⁡ θ s e c 3 θ c o s θ + s e n θ 3 s e c 3 θ d θ

1 3 ∫ 0 π 2 s e c 2 θ 1 + t g θ 3 d θ

Se aplicarmos o método de substituição fazendo u = 1 + t g θ , vamos obter que d θ = d u s e c 2 θ

1 3 ∫ 0 π 2 s e c 2 θ 1 + t g θ 3 d θ → 1 3 ∫ 1 u 3 d u

1 3 ∫ 1 u 3 d u = 1 3 - 1 2 u 2

Voltando u para 1 + t g θ

1 3 ∫ 0 π 2 s e c 2 θ 1 + t g θ 3 d θ = - 1 6 1 + t g θ 2 0 π 2

1 3 ∫ 0 π 2 s e c 2 θ 1 + t g θ 3 d θ = - 1 6 1 + t g π 2 2 - - 1 6 1 + t g 0 2

1 3 ∫ 0 π 2 s e c 2 θ 1 + t g θ 3 d θ = - 1 6 1 + ∞ 2 - - 1 6 1 + 0 2

Como 1 ∞ = 0 , temos

1 3 ∫ 0 π 2 s e c 2 θ 1 + t g θ 3 d θ = 1 6

E finalmente substituindo os resultados parciais das integrais na integral original do problema, temos

∫ 0 π 2 ∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r d θ = 1 3 ∫ 0 π 2 cos ⁡ θ d θ - 1 3 ∫ 0 π 2 cos ⁡ θ c o s θ + s e n θ 3 d θ

∫ 0 π 2 ∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r d θ = 1 3 - 1 6

∫ 0 π 2 ∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r d θ = 1 6

É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍

Resposta

∫ 0 π 2 ∫ 1 c o s θ + s e n θ 1 r 2 c o s θ d r d θ = 1 6

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x