UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 26
Calcule o volume limitado pelo parabolóide , pelo cilindro e pelo plano .
Passo 1
Eaew, belezinha?
Temos que calcular o volume limitado pelo parabolóide
acima do plano . E, delimitado lateralmente pelo cilindros circular
Este sólido é tal que
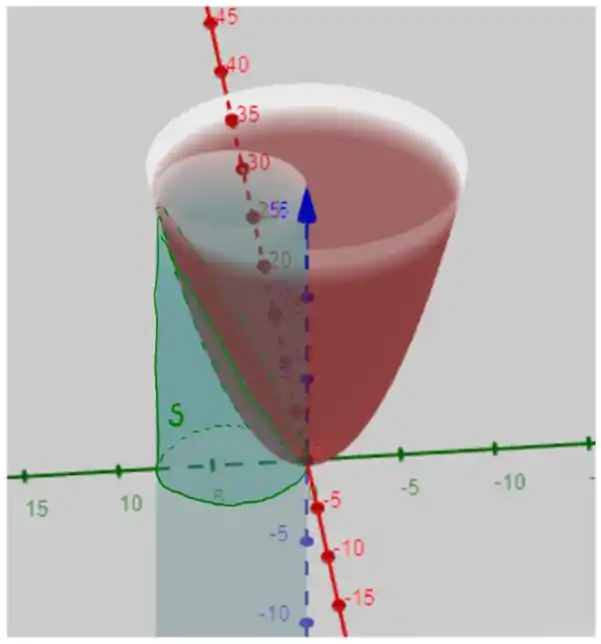
note que as laterais são o cilindro, a base é o plano e a tampa é o parabolóide , o volume pode ser calculado usando
em que . Vamos escrever a nossa função e reescrever a região , estabelecendo assim limites de integração! Saca só!
Passo 2
A função é dada pelo parabolóide que serve como tampa, temos que
O domínio é a circunferência que intercepta o plano dada simplesmente por
sendo assim, temos que resolver a seguinte integral
Os limites podem ser encontrados de maneira conveniente se usarmos coordenadas polares, mas como este cilindro é deslocado da origem, vamos primeiro reescrevê-lo!
Passo 3
Temos que a equação do cilindro é dada por
Se completarmos o quadrado, temos que
que é uma circunferência de raio fora da origem, vamos transladar a nossas coordenadas para obter
em que , como temos apenas uma translação, o jacobiano da mudança de coordenadas é
e, a nossa integral se torna
Agora sim podemos aplicar coordenadas polares! Vamos lá!
Passo 4
Aplicando coordenadas polares da forma
e
como o jacobiano da mudança de coordenadas é simplesmente dado por
temos que
como é uma circunferência completa, os limites são dados simplesmente por
Vamos resolver as integrações agora!
Passo 5
Vamos primeiro simplificar os integrandos, se distribuirmos o produtos, temos que
usando a identidade trigonométrica , temos que
Como os limites de integração são constantes (a região é retangular) temos que a ordem de integração não importa, então, vamos integrar primeiro em , temos que
usando que
e que
nos resta apenas as seguintes integrais
a integral em pode ser identificada como
e, também
de forma que temos
ou simplesmente
A questão é isso! Te vejo na próxima! Tchau Tchau!