UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 3
Nos exercícios 01 a 08, calcule , onde é a região descrita em cada caso
03. , a região do primeiro quadrante definida por , .
Passo 1
Suave na nave?! Tá complicada essa questão? Relaxa que a gente vai te ajudar!
Nesse problema, queremos obter a integral da função aplicada na região , onde é a região definida entre e .
E aí, tem ideia do que fazer? 🤔
O segredo é conseguir definir a região como os limites de integração de
Se conseguirmos fazer isso, a primeira integral deve ser definida entre duas funções e a última integral deve ser definida entre duas constantes.
Bora começar! 😁
Passo 2
Vamos começar esboçando a região .
é definida entre e e entre e , ou seja, tanto quanto é definido entre duas constantes, logo, é uma região retangular dada por
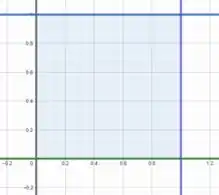
Assim, podemos montar nossa integral com e variando entre duas constantes, no caso, e .
Legal, né? 😊
Passo 3
Integrando com relação a , temos
Aplicando os limites de integração de ...
Integrando o resultado em relação a
Aplicando os limites de integração de
O que achou? Foi de boa? Responde aí! 😊
