UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Prof° Edison Figueiredo - 1ª Lista, Questão 16
Se , mostre que .
(Sugestão: Faça e )
Passo 1
Oiie, tudo certinho contigo?
Temos que mostrar que a partir da seguinte integração
sobre o domínio limitado de forma que
é possível mostrar que
O segredo é avaliar os limites de integração baseados no domínio indicado como a região , no entanto, nestas coordenadas a integração pode ser complicada, aí entra a sugestão dada, em que podemos tentar fazer a seguinte substituição para simplificar o problema
e
e assim obter uma nova região que pode simplificar o nosso problema! Vamos fazer isso agora!
Passo 2
Primeiro vamos tentar visualizar a nossa região de integração
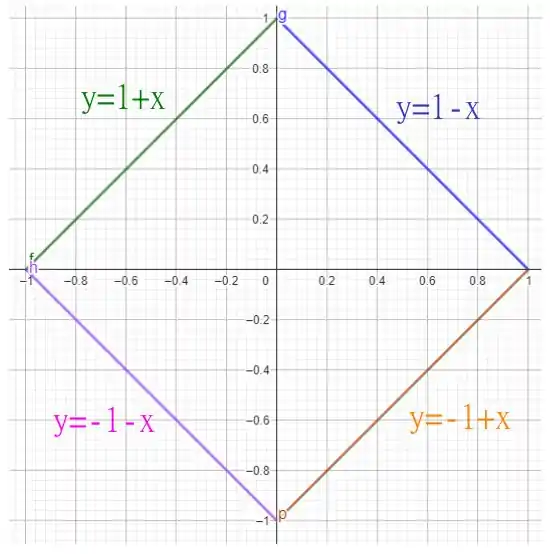
note que montar as quatro retas que determinam a região, é preciso usar a seguinte relação
mas note que a definição de módulo indica que para , temos que , e temos que para , , pode se fazer analogamente para , e assim se obtém as quatro retas indicadas acima! Isso vai ser importante quando formos escrever nossa nova regi��o! Vamos fazer agora a mudança de coordenadas sugerida!
Passo 3
Foi sugerido que fizéssemos
e
ao fazer uma mudança de coordenadas, temos que
em que
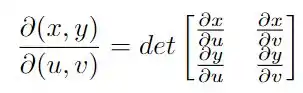
que é o jacobiano da mudança de coordenadas, para aplicarmos a definição precisamos obter e , isso é obtido subtraindo ambas equações em de forma que
e como temos que
de forma que podemos aplicar o determinante do jacobiano para obter
ou simplesmente
Usando estes resultados e a mudança de coordenadas em nossa integral dupla, temos que
Bem mais simples não é? Faltam só os limites de integração! Para isso, vamos visualizar quem é a região !
Passo 4
Ao fazer a mudança de coordenadas nós mudamos nossa região, antes delimitadas por quatro retas, mas agora, estas quatro retas se tornam
ou simplesmente
uma reta de inclinação positiva! Analogamente para as outras retas, temos que
nos leva à
e, também que
e
que é a seguinte região
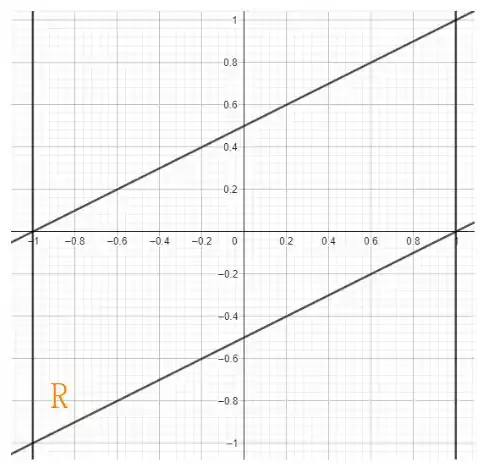
Os limites de integração são então simplesmente dados por
Ficou bem mais simples que a integral original não é? Como os limites não são constantes (a região não é retangular), temos que integrar primeiro em , já que os seus limites dependem da outra variável! Vamos fazer isso!
Passo 5
Vamos começar com a integral em , temos que
já que depende apenas de , obtemos que
ou simplesmente
Temos então que
de forma que a integral é
A questão foi isso! Te vejo na próxima! Tchau Tchau!