Calcule a área comum aos círculos limitados por e .
Passo 1
Oiie, tudo bem?
Precisamos calcular a área da seguinte região delimitada pelas circunferências
e
A região é tal que
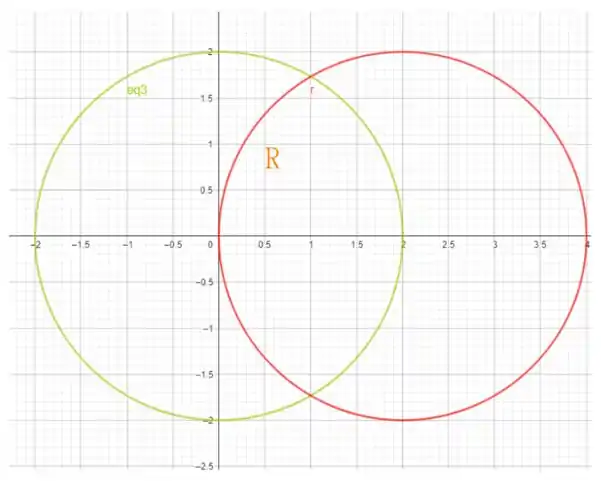
O cálculo da área pode ser feito utilizando integração dupla como
Ou seja, é apenas o trabalho de calcular os limites de integração! Neste caso será conveniente reescrever o sistema usando coordenadas polares. Saca só!
Passo 2
Em coordenadas polares da forma
e
com jacobiano dado por
temos que a primeira circunferência é descrita simplesmente por
e, expandindo o quadrado na segunda circunferência, temos que
ou simplesmente
A interseção entre as duas curvas acontece quando . Ou seja, quando
Isso é válido para dois ângulo devido a paridade do cosseno, os ângulos são
Vamos usar essa região para escrever a nossa integral!
Passo 3
A coordenada radial vai de (primeira circunferência) até , devido a interseção, o ângulo está entre e , sendo assim, temos que calcular
Como os limites não são constantes (a região não é retangular) temos que a ordem da integração importa, precisamos integrar primeiro em pois seus limites dependem de , integrando em , temos que
Ou seja, nos resta resolver
Vamos fazer isso agora!
Passo 4
Para resolver a primeira integral, vamos usar a relação de meio ângulo para o cosseno, temos que
temos que
convenientemente esse resultado pode ser usado novamente para calcular a nossa área (então anote ele em algum cantinho), temos também que
em que usei a paridade do seno para escrever este resultado. A área é então dada por
como temos que , obtemos finalmente
A questão foi isso! Te vejo na próxima! Tchau Tchau!