UFPB, Sem Campus, Cálculo Diferencial e Integral III, Listas de Cálculo 3 - Profº Edson Figueiredo - 1ª Lista, Questão 13
13. Escreva
como uma integral dupla e esboce graficamente a região de integração correspondente.
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão nosso objetivo é reescrever a integral dada em forma de integral dupla definida e esboçar a região de integração.
E aí, como podemos fazer isso? 🤔
A integral dada é , a partir dela podemos ver que é definido entre e , mas precisamos obter outra integral antes da integral de .
Bora ver como fazemos isso? 😎
Passo 2
A função que aparece dentro da integral é a função , ou seja, temos que obter uma integral que resulte em .
Sabemos que a integral de uma função qualquer definida em um intervalo é dada por
O podemos perceber dessa função de integração é que os limites de integração e , são no nosso caso e .
E qual é a função que quando integrada resulta em ? A derivada de , não é?
Então , pelo teorema fundamental do cálculo, vemos que
Assim, montando a integral dupla
Onde , e , temos
Entendeu essa parte? 😉
Passo 3
Agora vamos obter o gráfico da região de integração.
Pra isso, podemos ver na integral que varia no intervalo e varia entre .
Esboçando as equações , , e , temos
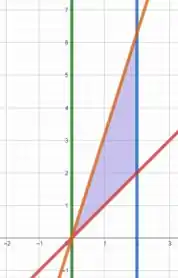
Então a região hachurada em roxo é a nossa região de integração.
É isso! Essa resolução te ajudou? Responde Aí! ✌
