Fundamentos de Física – Halliday e Resnick. 9° Ed. Volume 1. Seção 8.5, Questão 35.
Na Fig. 8-40, um bloco de massa desliza para baixo, a partir do repouso, percorre uma distância em um plano inclinado de ângulo e se choca com uma mola de constante elástica . Quando o bloco para momentaneamente, a mola fica comprimida . Quais são (a) a distância e (b) a distância entre o ponto do primeiro contato do bloco com a mola e o ponto onde a velocidade do bloco é máxima?
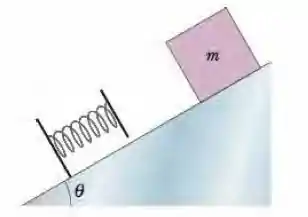
Figura 8-40 Problema 35
Passo 1
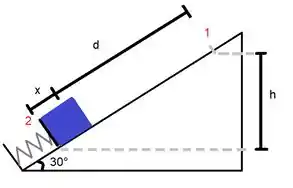
a) A figura mostra o instante em que o bloco para momentaneamente. Nesse momento, toda a energia potencial gravitacional que o bloco possuía no início foi transformada em energia potencial elástica (lei da conservação de energia).
A distância total percorrida pelo bloco no plano inclinado é . Tomando como ponto de referência para a energia potencial o ponto onde o bloco para, a altura do bloco no ponto 1 é
Logo
Para , , , e
Passo 2
b) Para encontrar a velocidade máxima, deve-se encontrar instante em que a aceleração se torna zero, pois em seguida ela muda de sentido, desacelerando o movimento. Nesse instante as forças agindo no bloco são a componente da força peso paralela ao plano inclinado () e a força da mola ().
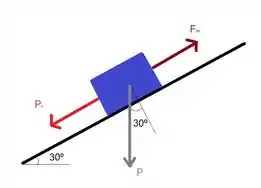
Se a aceleração é zero, então a resultante das forças paralela ao plano inclinado será nula. Adotando a descida do bloco como positivo
Resposta
a)
b)