Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
Halliday - Vol.1 - Ed. 8 - Capítulo 8 – Seção 5 – Questão 29.
(Capítulo 8.5 – Exercício 29) Um bloco de massa é apoiado em uma mola em um plano inclinado sem atrito de ângulo (Fig. 8-42). (O bloco não está preso à mola.) A mola, de constante elástica , é comprimida e depois liberada. (a) Qual é a energia potencial elástica da mola comprimida? (b) Qual é a variação da energia potencial gravitacional do sistema bloco – Terra quando o bloco se move do ponto em que foi liberado até o ponto mais alto que atinge no plano inclinado? (c) Qual é a distância percorrida pelo bloco ao longo do plano inclinado até atingir a altura máxima?
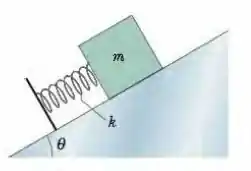
Figura 8-42 Problema 31
Passo 1
Faaala gente, vamos pra mais uma questão!!
a) Vamos tomar como referência da energia potencial gravitacional o instante em que a compressão da mola é máxima, beleza?
A energia potencial elástica nesse ponto é
Para e , temos
Showw demais, já encontramos a energia potencial elástica quando a mola está comprimida 😉 agora vamos encontrar essa energia no ponto mais alto
Passo 2
b) No ponto mais alto, toda a energia potencial elástica inicial é transformada em energia potencial gravitacional ()
Ou seja, aquele valor que encontramos no item anterior será convertido em energia potencial gravitacional quando formos pro ponto mais alto, logo
Passo 3
c) Pra fechar, queremos a distância percorrida pelo bloco
Pela conservação de energia, temos
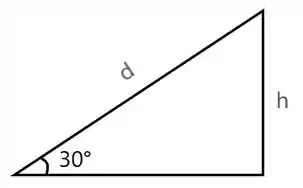
Como a distância é ao longo do plano, vamos usar trígonometria
Arrasamos!
Resposta
a)
b)
c)