Na Fig. 8 - 52, um bloco desliza ao longo de uma pista, de um nível para outro mais elevado, passando por um vale intermediário. A pista não possui atrito até o bloco atingir o nível mais alto, onde uma força de atrito para o bloco depois que ele percorre uma distância . A velocidade inicial do bloco é a diferença de altura é e é . Determine o valor de.
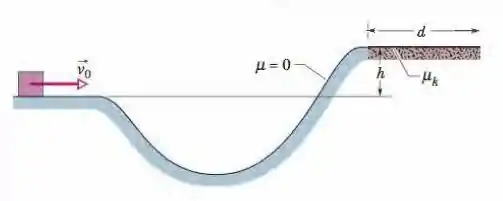
Figura 8-52 Problema 57.
Passo 1
Vamos primeiro considerar o ponto inicial como tem energia potencial gravitacional nula. Dessa forma, a energia neste ponto é:
Quando o bloco sobe a altura h e passa pelo chão que possui atrito temos uma energia mecânica
Desta forma, a variação da energia mecânica é:
Passo 2
Como existe uma força dissipativa (o atrito) a lei de conservação passa a ser:
Mas para o caso do atrito temos:
Como a força de atrito é contrária ao movimento do bloco, seu atrito é negativo:
Pelo equilíbrio das forças na vertical, temos
Dessa forma
E então, a energia dissipada é:
Passo 3
Usando a lei de conservação da energia, temos:
Simplificando os termos de :
Para , , e
Resposta
A distância percorrida até o bloco parar é de .