Exercícios Resolvidos de Energia Cinética + Energia Gravitacional + Energia Elástica
Ver TeoriaEnunciado
Halliday - Vol.1 - Ed. 8 - Capítulo 8 – Seção 5 – Questão 22.
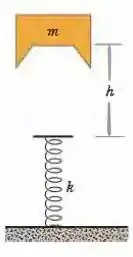
(Capítulo 8.5 – Exercício 22) Um bloco de massa é deixado cair de uma altura sobre uma mola de constante elástica . Determine a variação máxima de comprimento da mola ao ser comprimida.
Passo 1
Oláááá, vamos lá pra mais um probleminha de energia?
Primeiramente, vamos chamar de a compressão sofrida pela mola devido a queda do bloco e tomar como referência essa posição final do bloco
Temos então que a altura total de queda () é dado por
Pelo princípio de conservação de energia mecânica
Onde representa a energia cinética do sistema, representa a energia potencial (gravitacional e/ou elástica) e os subíndices referem-se aos diferentes instantes de um processo de transferência de energia.
Então vamos lá?
Passo 2
Na posição inicial há apenas energia potencial gravitacional () e na posição final apenas a energia potencial elástica (), logo
Substituindo , , e
Passo 3
Agora, basta apenas resolver a nossa equação do segundo grau, com , e .
Ou seja, a variação máxima de comprimento é 😊