Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Posição do Centro de Massa

Ver Teoria
Exercício 46123456789101112131415161718192021222324252627282930313233343536373839404142434445474849505152535455565758596061626364656667686970

Enunciado

Fundamentos de Física – Mecânica. Halliday e Resnick. 9ª edição. Capítulo 9, exercício 7.

Na molécula de amônia ( N H 3 ) da Fig. 9-40, três átomos de hidrogênio (H) formam um triângulo equilátero, com o centro do triângulo a uma distância d = 9,40 × 10 - 11   m de cada átomo de hidrogênio. O átomo de nitrogênio (N) está no vértice superior de uma pirâmide, com os três átomos de hidrogênio formando a base. A razão entre as massas de nitrogênio e do hidrogênio é 13,9 e a distância nitrogênio-hidrogênio é L = 10,14 × 10 - 11   m . Quais são as coordenadas (a) x e (b) y do centro de massa da molécula?

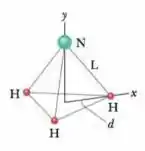
Passo 1

Para calcular a coordenada de cada eixo do centro de massa podemos usar as seguintes relações:

x c m = m 1 x 1 + m 2 x 2 + m 3 x 3 + m 4 x 4 m 1 + m 2 + m 3 + m 4

y c m = m 1 y 1 + m 2 y 2 + m 3 y 3 + m 4 y 4 m 1 + m 2 + m 3 + m 4

Porém, devemos prestar atenção para o caso de haver simetria na peça. Neste caso, percebemos que o eixo y corta exatamente nossa peça ao meio.

Passo 2

Portanto, para calculcar a coordenada x do centro de massa, não precisamos aplicar a expressão dada no passo anterior. Devemos perceber que o centro de massa da peça está localizado no eixo de simetria que é o eixo y . Assim:

x c m = 0

Passo 3

Para determinar a coordenada y do centro de massa, usaremos a expressão dada no passo inicial:

y c m = m 1 0 + m 2 0 + m 3 0 + m N y N m N + 3 m H

y c m = m N y N m N + 3 m H

Isolando y N , temos:

y c m m N m N + 3 y c m m H m N = y N

Como o desenho é formado por triângulos retângulo, podemos aplicar o teorema de pitágoras para determinar o y N :

y N 2 + d 2 =   L 2 → y N = L 2 - d 2

y N =   10,14 × 10 - 11 2 - 9,4 × 10 - 11 2 = 3,80 × 10 - 11   m

E foi dado que a relação entre a massa de nitrogênio e de hidrogênio é m N m H =   13,9 . Assim, devolvendo em nossa expressão, temos:

y c m + 3 y c m 13,9 = 3,80 × 10 - 11

13,9 + 3 y c m 13,9 = 3,80 × 10 - 11

Isolando y c m :

y c m = 3,80 × 10 - 11 × 13,9 16,9 = 3,13 × 10 - 11   m

Resposta

  1. x c m = 0 ;
  2. y c m = 3,13 × 10 - 11   m .

Exercícios de Livros Relacionados

A Fig. 9-35 mostra um sistema de três partículas de massas m 1 = 3,0k g , m 2 = 4,0k g e m 3 = 8,0k g . As escalas do gráfico são definidas por x s = 2,0m e y s = 2,0m . Quais são (a) a coordenada x e
Um pedaço uniforme de folha de metal é moldado conforme mostrado na Figura P8.34. Calcule as coordenadas x e y do centro de massa da folha.
Uma haste de 30,0c m de comprimento tem densidade linear (massa por comprimento) definida por λ=50,0+20,0x em que x é a distância a partir de uma extremidade, medida em metros, e λ expressa g r a m a
Duas partículas de 3,0k g têm velocidades v → 1 = 2,0 m s i ^ + 3,0 m s j ^ e v → 2 = 4,0 m s i ^ - 6,0 m s j ^ . Encontre a velocidade do centro de massa do sistema.
Quatro corpos estão situados ao longo do eixo y da seguinte forma: um de 2,00k g está a + 3,00m , um de 3,00k g está a + 2,50m , o terceiro, de 2,50k g , está na origem, e o quarto, de 4,00k g , está