UFSCAR – Cálculo I – Listas - Teste 9 – Lista de Estudos Cálculo 1 - UFSCAR – Lista 1 – Versão 2 Questão 1a
Em cada item abaixo, determine os valores reais de que satisfazem as inequações.
a)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma inequação e pede para determinarmos quais os valores de para que seja sempre maior ou igual a zero.
Mas como podemos determinar esses valores?
Bom... uma alternativa é dividirmos a fração em duas funções distintas e analisar cada uma!
Se não entendeu, então vamos aqui juntos!!
Passo 2
Fazendo , temos uma função a fim dada pela seguinte reta:
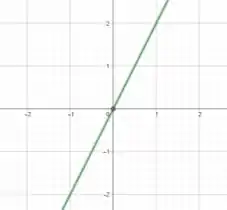
E, fazendo , temos a seguinte parábola:
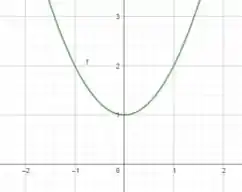
Agora precisamos definir para que .
Passo 3
Bom... para que , temos que tem que ser maior que zero, já que é sempre maior que zero (como pode-se observar a parábola sempre no semieixo positivo).
Olhando o gráfico de , vemos que quando , a condição é atendida!!
Entendeu direitinho? Responde aee ;)
