2. O valor de tal que
Pertence ao intervalo:
a)
b)
c)
d)
e)
Passo 1
Falaaa... tudo bem??
Nessa questão vamos achar qual o valor de para que
E depois dizer a qual intervalo, entre as opções, ele pertence.
Repara que se substituirmos na expressão dentro do limite, vamos achar alguma coisa dividida por zero. Maaaas sabemos que o limite existe e é igual a 3, então conseguimos dividir o polinômio de cima por e ter resto igual a zero.
Passo 2
Fazendo a divisão polinomial:
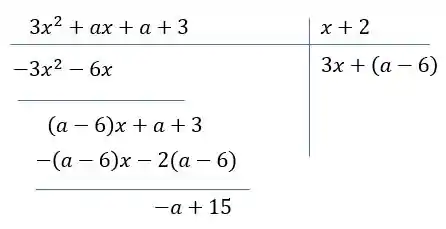
Encontramos o resto: , mas ele deve ser igual a zero, então:
Então pertence ao intervalo de .
Letra e
Resposta
Letra e