UFSCAR – Cálculo I – Listas - Teste 9 – Lista de Estudos Cálculo 1 - UFSCAR – Lista 1 – Versão 2 Questão 4e
Em cada um dos itens abaixo, determine o domínio da função dada.
e)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar o domínio da função .
Mas o que é esse tal de domínio??
Bom.. Dada a função que relaciona os elementos do conjunto aos elementos do conjunto , podemos definir:
O conjunto é conhecido como domínio e esse nome é escolhido para esse conjunto devido ao papel dos seus elementos na função.
Lembre-se de que o conjunto é que determina a variável independente.
Portanto, os elementos do conjunto possuem o “domínio” sobre os resultados da função, uma vez que os resultados de obtidos dependem do valor escolhido.
Agora vamos juntos determinar o domínio da função!! 😉
Passo 2
Bom... para que a função exista em , devemos ter e .
Dessa forma, temos dois casos:
Passo 3
Já para , fazendo o estudo do sinal, temos:
- Para , temos:
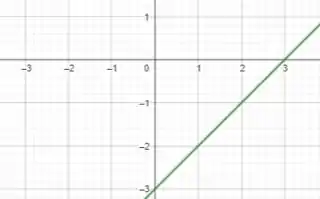
E, para , temos:
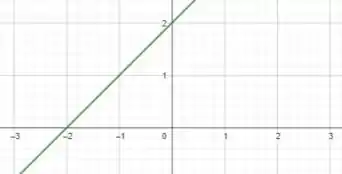
Assim, para , então temos que ter:
Dessa forma, unindo os casos, temos que:
Entendeu direitinho? Responde aee ;)
