UFSCAR – Cálculo I – Listas - Teste 9 – Lista de Estudos Cálculo 1 - UFSCAR – Lista 1 – Versão 2 Questão 1b
Em cada item abaixo, determine os valores reais de que satisfazem as inequações.
b)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma inequação e pede para determinarmos quais os valores de para que seja sempre menor que zero.
Mas como podemos determinar esses valores?
Bom... uma alternativa é dividirmos a fração em duas funções distintas e analisar cada uma!
Se não entendeu, então vamos aqui juntos!!
Passo 2
Fazendo , temos uma função a fim dada pela seguinte reta:
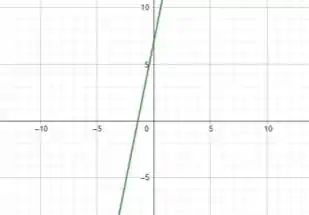
Onde o ponto em que a reta toca o eixo é .
E, fazendo , temos a seguinte reta:
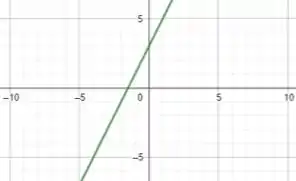
Onde o ponto em que a reta toca o eixo é .
Agora precisamos definir para que .
Passo 3
Bom... para que , temos que encontrar o intervalo de para o qual as frações possuem sinais opostos.
Dessa forma, podemos ver que isso ocorre no intervalo .
Entendeu direitinho? Responde aee ;)
